分类模型不仅会告诉你它们认为答案是什么，还会告诉你它们对这个答案有多确定。这种确定性以概率得分的形式表示。高分意味着模型非常自信，而低分则意味着它对预测结果不确定。

每个分类模型计算这些概率得分的方式都不同。简单模型和复杂模型各自有确定每种可能结果可能性的特定方法。

我们将探索七种基本的分类模型，并直观地分解每种模型是如何计算出其概率得分的。

定义

预测概率（或“类别概率”）是一个从0到1（或从0%到100%）的数字，表示模型对其答案的置信程度。如果数字是1，则模型对其答案完全确定。如果它是0.5，则模型基本上是在猜测——就像抛硬币一样。

概率得分的组成部分

当模型需要在两个类别之间做出选择时（称为二分类），适用以下三个主要规则：

1. 预测概率必须在0和1之间。
2. 两个选项发生的可能性之和必须等于1。
3. 概率越高，意味着模型对其选择越确定。

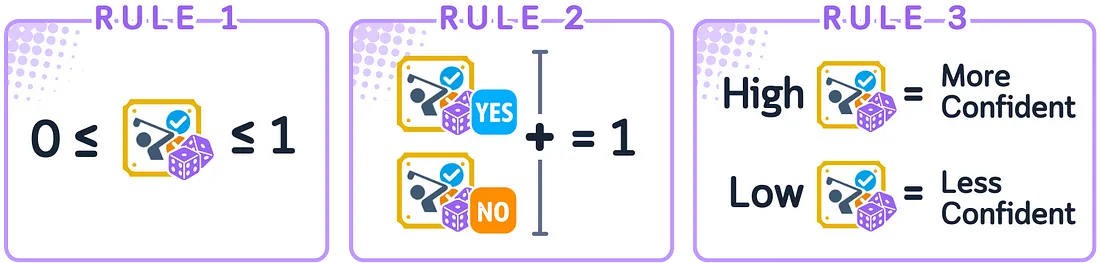
对于二分类问题，当我们谈论预测概率时，通常指的是正类的概率。较高的概率意味着模型认为正类更可能出现，而较低的概率则意味着模型认为负类更可能出现。

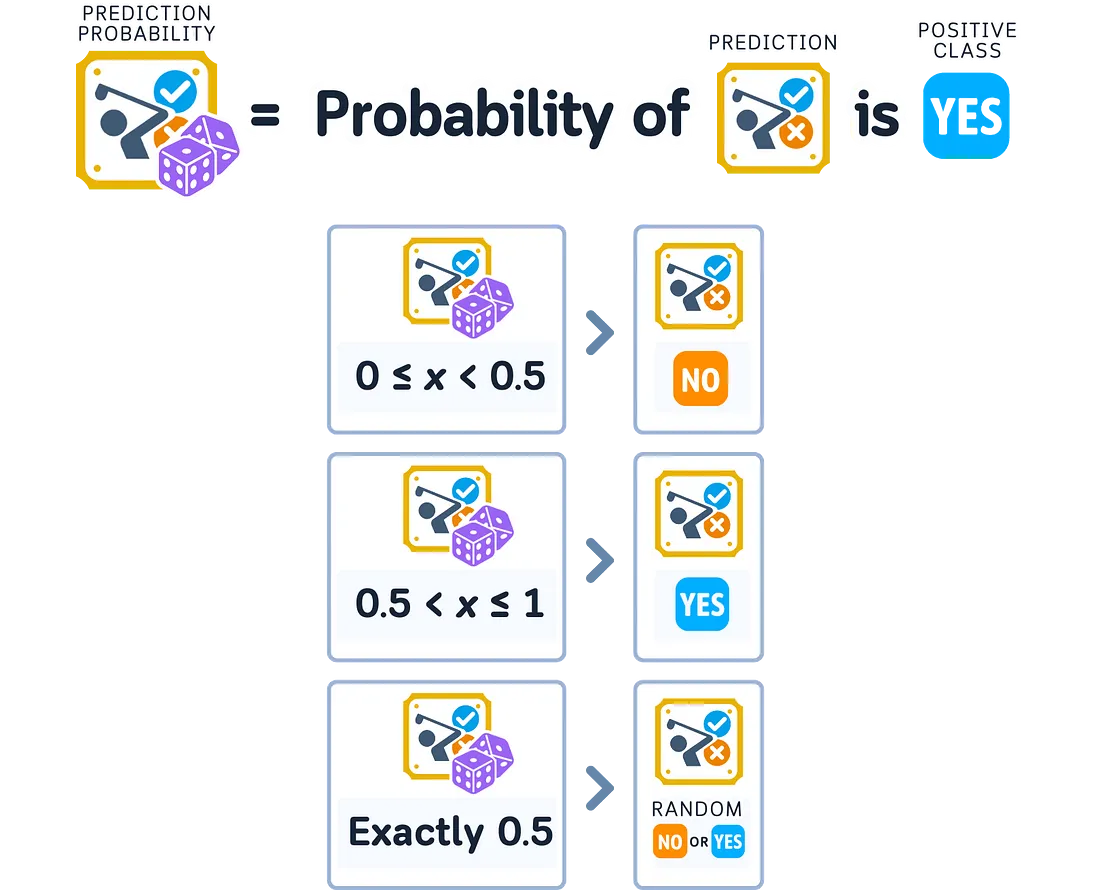
为了确保遵循这些规则，模型使用数学函数将其计算结果转换为适当的概率。每种类型的模型可能会使用不同的函数，这会影响它们如何表达置信度。

预测与概率

在分类中，模型会选择它认为最有可能发生的类别——即具有最高概率得分的类别。但两个不同的模型可能会选择相同的类别，同时对它的置信度却有所不同。它们的预测概率得分告诉我们每个模型的确定程度，即使它们做出了相同的选择。

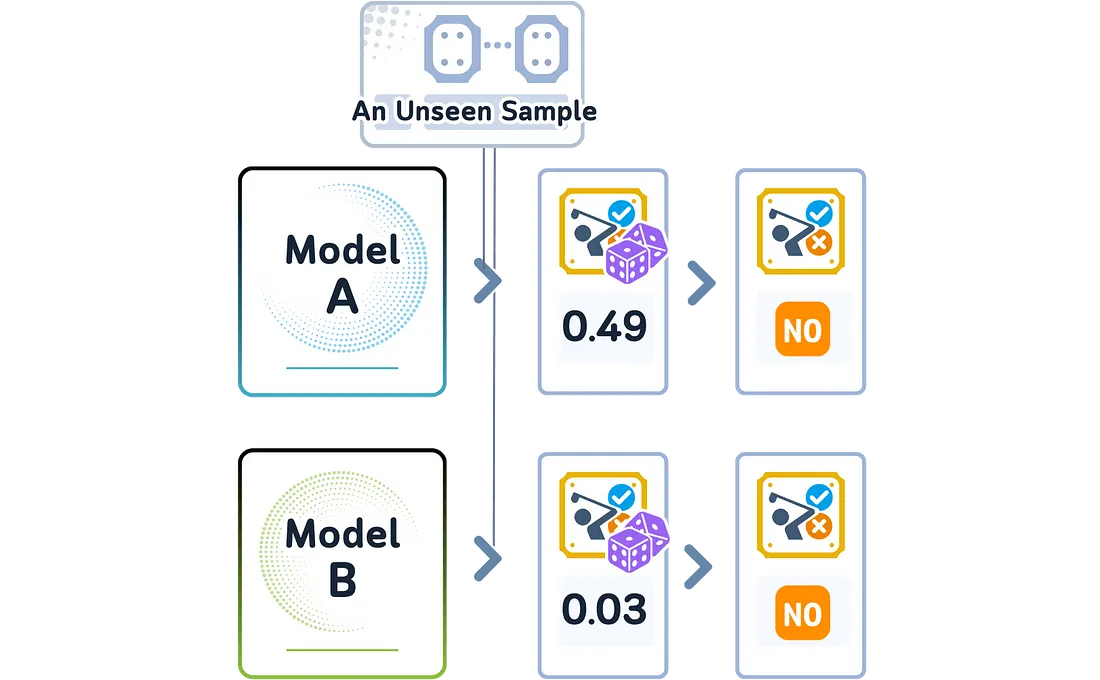
这些不同的概率得分向我们传达了一个重要信息：即使模型选择了相同的类别，它们可能对数据的理解也不同。

一个模型可能对其选择非常确定，而另一个模型可能不太确定——即使它们做出了相同的预测。

使用的数据集

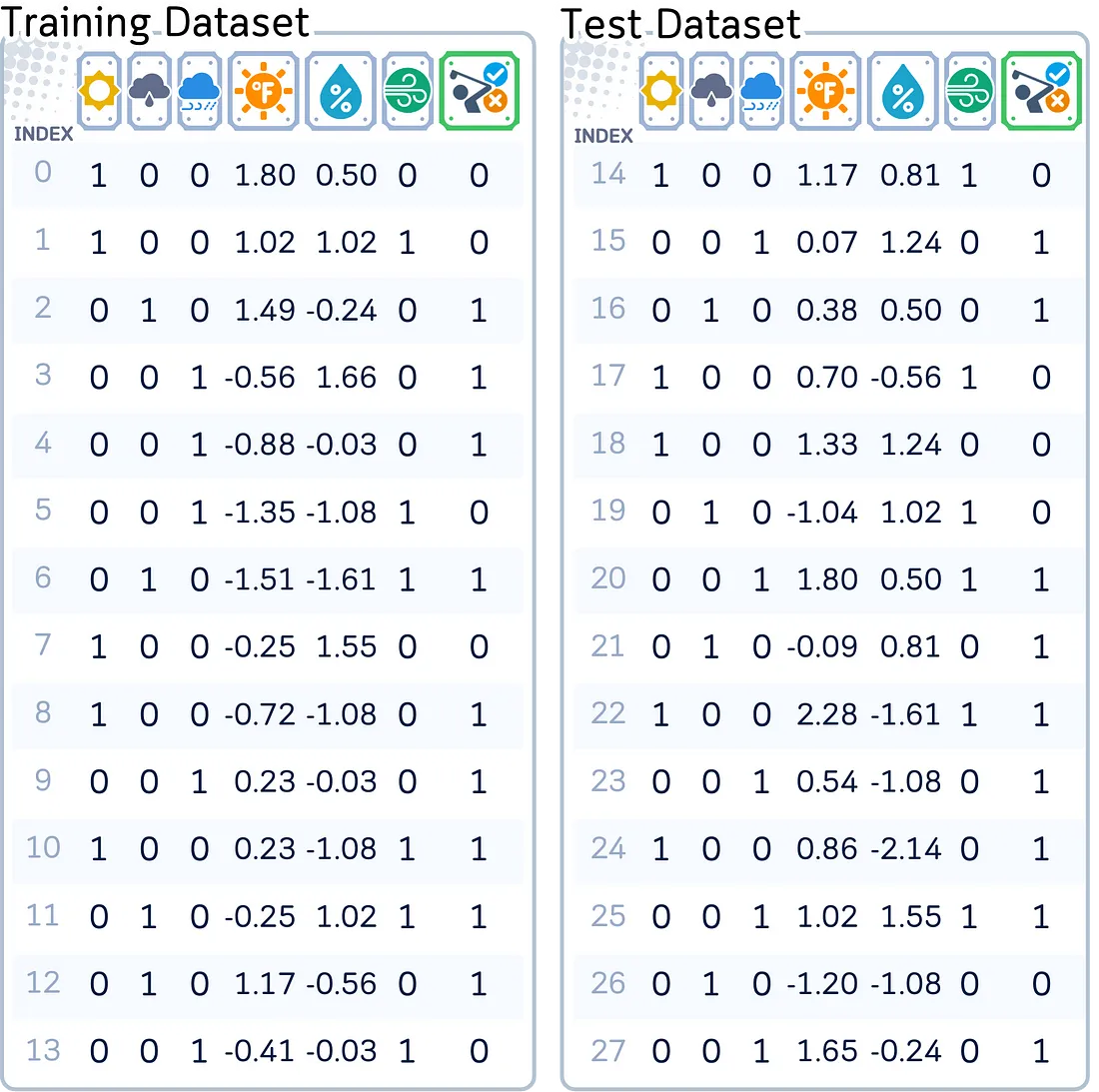
为了理解预测概率是如何计算的，我们将继续使用我在之前关于分类算法的文章中使用的相同数据集。我们的目标仍然是：根据天气情况预测某人是否会去打高尔夫球。

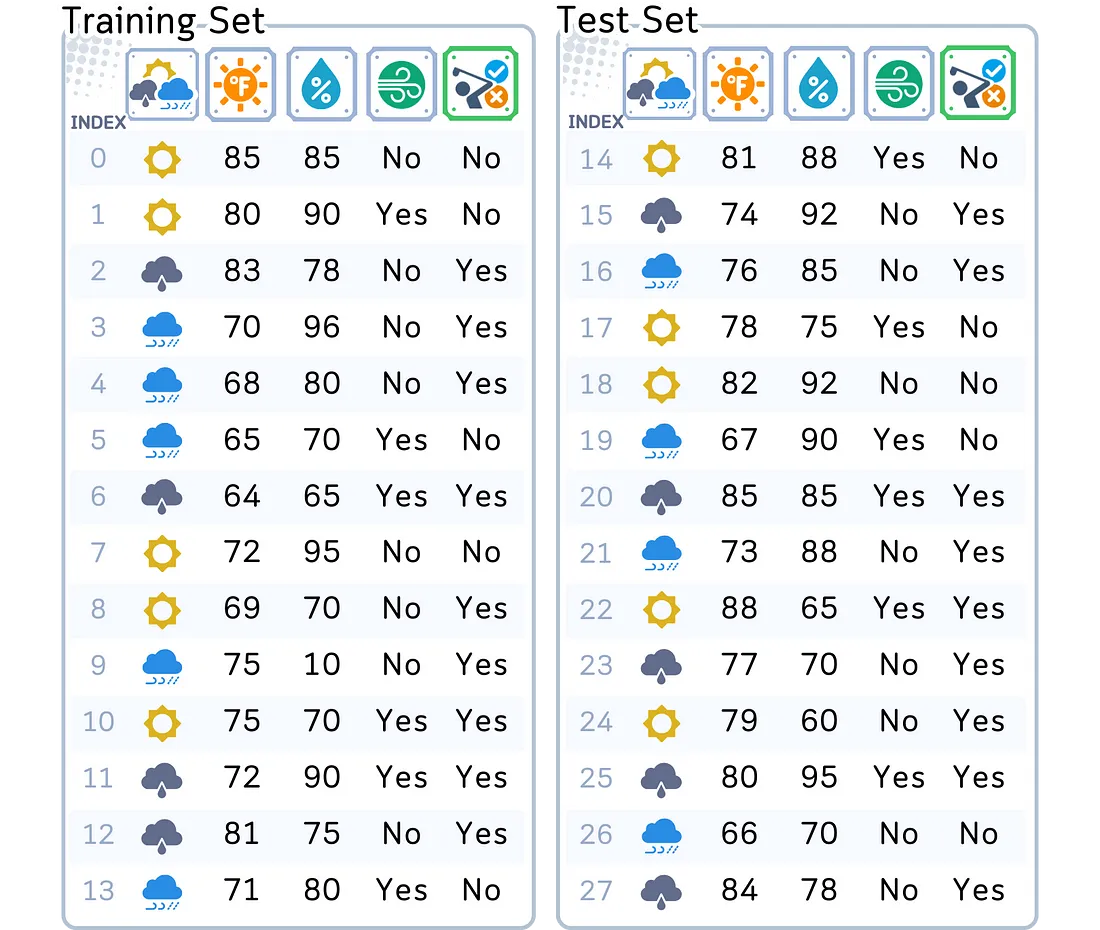
import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# Create and prepare dataset
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rainy', 'rainy', 'rainy', 'overcast', 
                'sunny', 'sunny', 'rainy', 'sunny', 'overcast', 'overcast', 'rainy',
                'sunny', 'overcast', 'rainy', 'sunny', 'sunny', 'rainy', 'overcast',
                'rainy', 'sunny', 'overcast', 'sunny', 'overcast', 'rainy', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,
                   72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,
                   88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,
                 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,
                 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True,
             True, False, True, True, False, False, True, False, True, True, False,
             True, False, False, True, False, False],
    'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes',
             'Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes',
             'Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}
# Prepare data
df = pd.DataFrame(dataset_dict)

由于某些算法可能需要标准化的值，我们还将对数值特征进行标准化处理，并对包括目标特征在内的类别特征进行独热编码（one-hot encoding）。

from sklearn.preprocessing import StandardScaler
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)
# Rearrange columns
column_order = ['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind', 'Play']
df = df[column_order]
# Prepare features and target
X,y = df.drop('Play', axis=1), df['Play']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Scale numerical features
scaler = StandardScaler()
X_train[['Temperature', 'Humidity']] = scaler.fit_transform(X_train[['Temperature', 'Humidity']])
X_test[['Temperature', 'Humidity']] = scaler.transform(X_test[['Temperature', 'Humidity']])

现在，让我们来看看以下7种分类算法是如何计算这些概率的：

哑分类器概率

哑分类器（Dummy Classifier）是一种不从数据中学习模式的预测模型。相反，它遵循一些基本规则，比如：选择最常见的结果、根据每个结果在训练中出现的频率进行随机预测、总是选择一个答案、或者在选项之间以相等的概率随机选择。哑分类器会忽略所有输入特征，只是遵循这些规则。

当这个模型完成训练后，它所记住的只是几个数字，这些数字要么显示了每个结果发生的频率，要么显示了它被指示使用的常数值。它不会学习任何关于特征如何与结果相关联的知识。

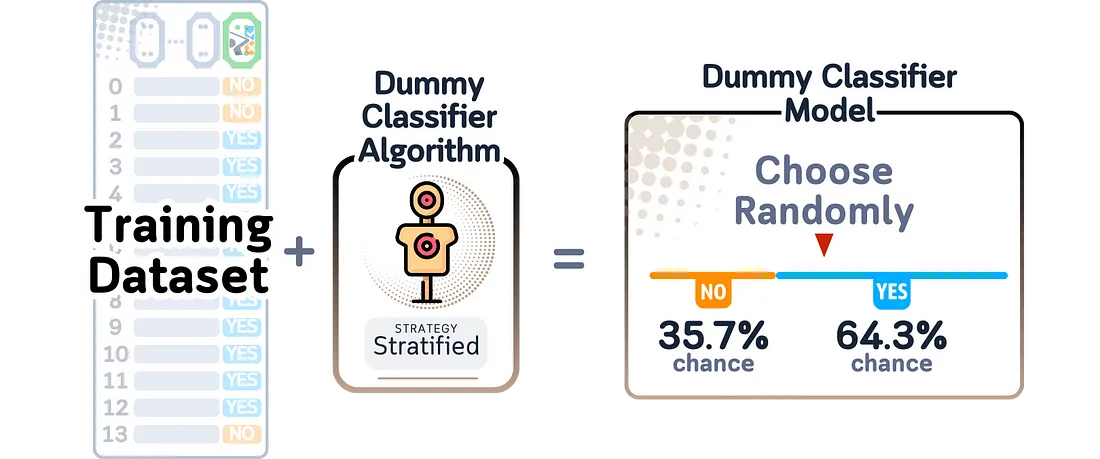
在二分类问题中计算预测概率时，哑分类器（Dummy Classifier）采用尽可能基础的方法。由于它只记住了每个结果在训练数据中出现的频率，因此它将这些相同的数字作为每个预测的概率得分——要么是0，要么是1。

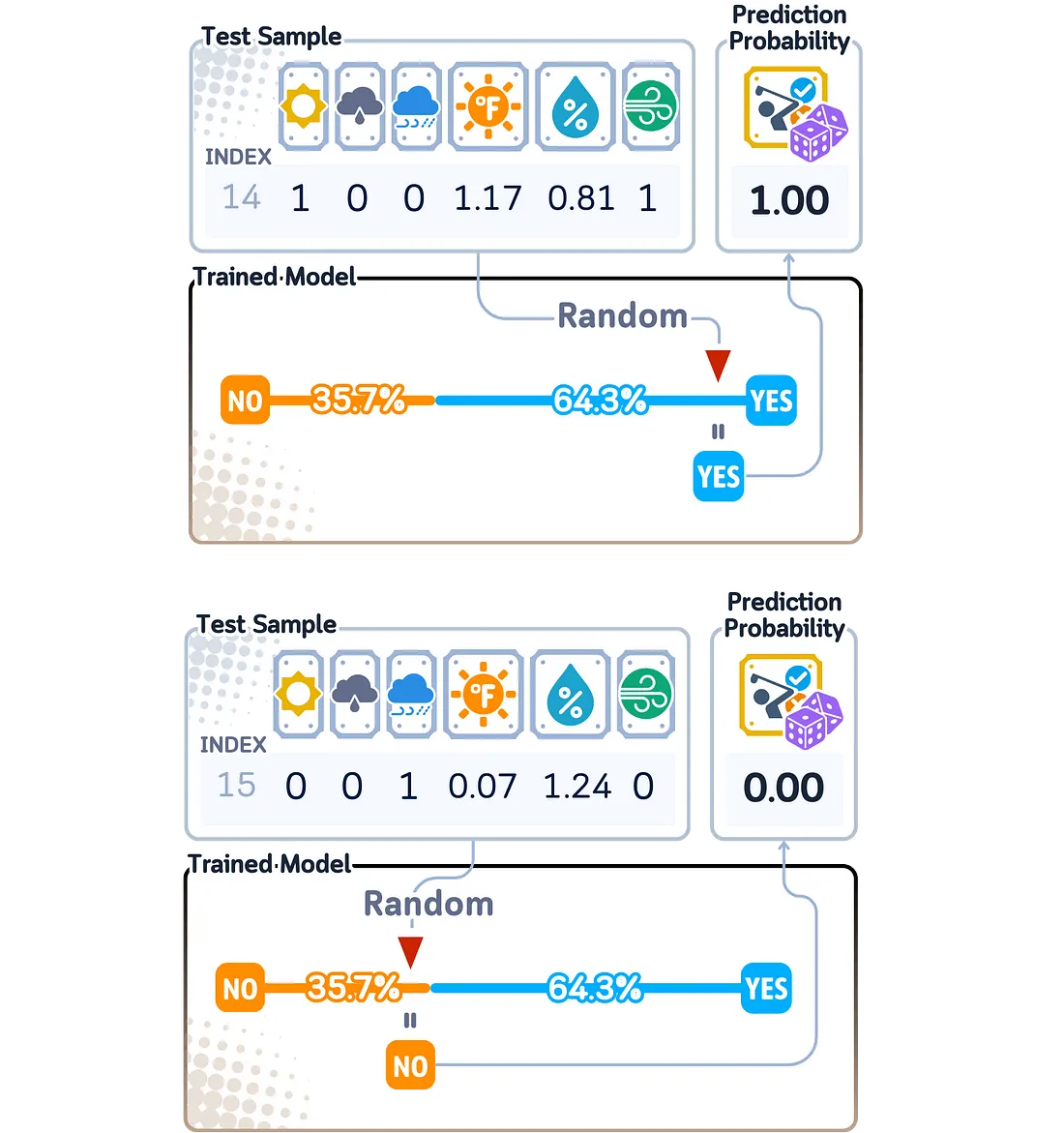
这些概率得分对于所有新数据都保持不变，因为模型不会查看或响应它试图预测的新数据的任何特征。

from sklearn.dummy import DummyClassifier
import pandas as pd
import numpy as np
# Train the model
dummy_clf = DummyClassifier(strategy='stratified', random_state=42)
dummy_clf.fit(X_train, y_train)
# Print the "model" - which is just the class probabilities
print("THE MODEL:")
print(f"Probability of not playing (class 0): {dummy_clf.class_prior_[0]:.3f}")
print(f"Probability of playing (class 1): {dummy_clf.class_prior_[1]:.3f}")
print("\nNOTE: These probabilities are used for ALL predictions, regardless of input features!")
# Make predictions and get probabilities
y_pred = dummy_clf.predict(X_test)
y_prob = dummy_clf.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
    'True Label': y_test,
    'Prediction': y_pred,
    'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

k-最近邻（KNN）概率

K-最近邻（kNN）是一种采用不同方法的预测模型——它不是学习规则，而是将所有训练样本保存在内存中。当需要对新数据进行预测时，它会衡量新数据与每个存储样本的相似度，找出k个最相似的样本（其中k是我们选择的一个数），并基于这些邻居做出决策。

当这个模型完成训练后，它所存储的全部内容就是完整的训练数据集、我们选择的k值以及一种衡量两个数据点相似度的方法（默认使用欧氏距离）。

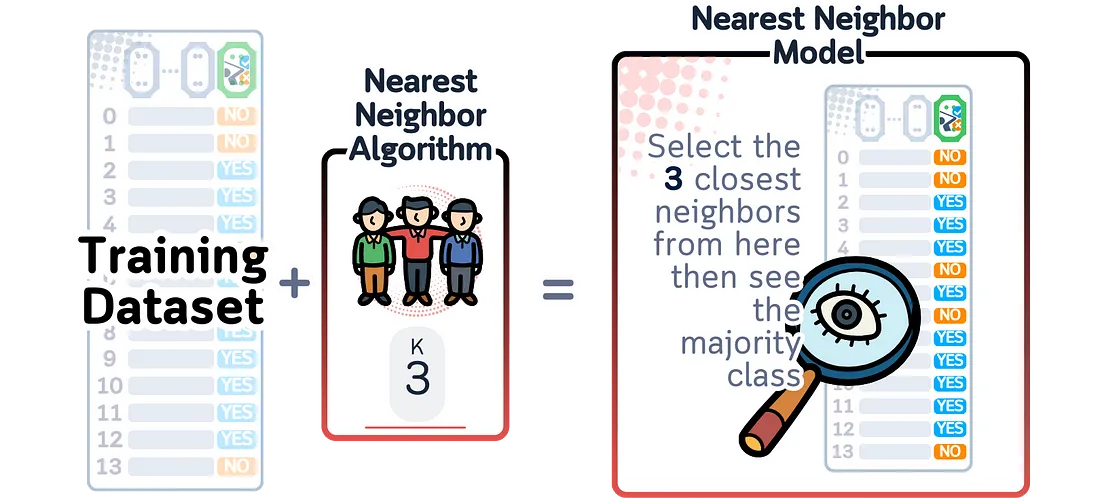
为了计算预测概率，kNN会查看那些k个最相似的样本，并统计每个类别中有多少个这样的样本。概率得分就是属于某个类别的邻居数量除以k。

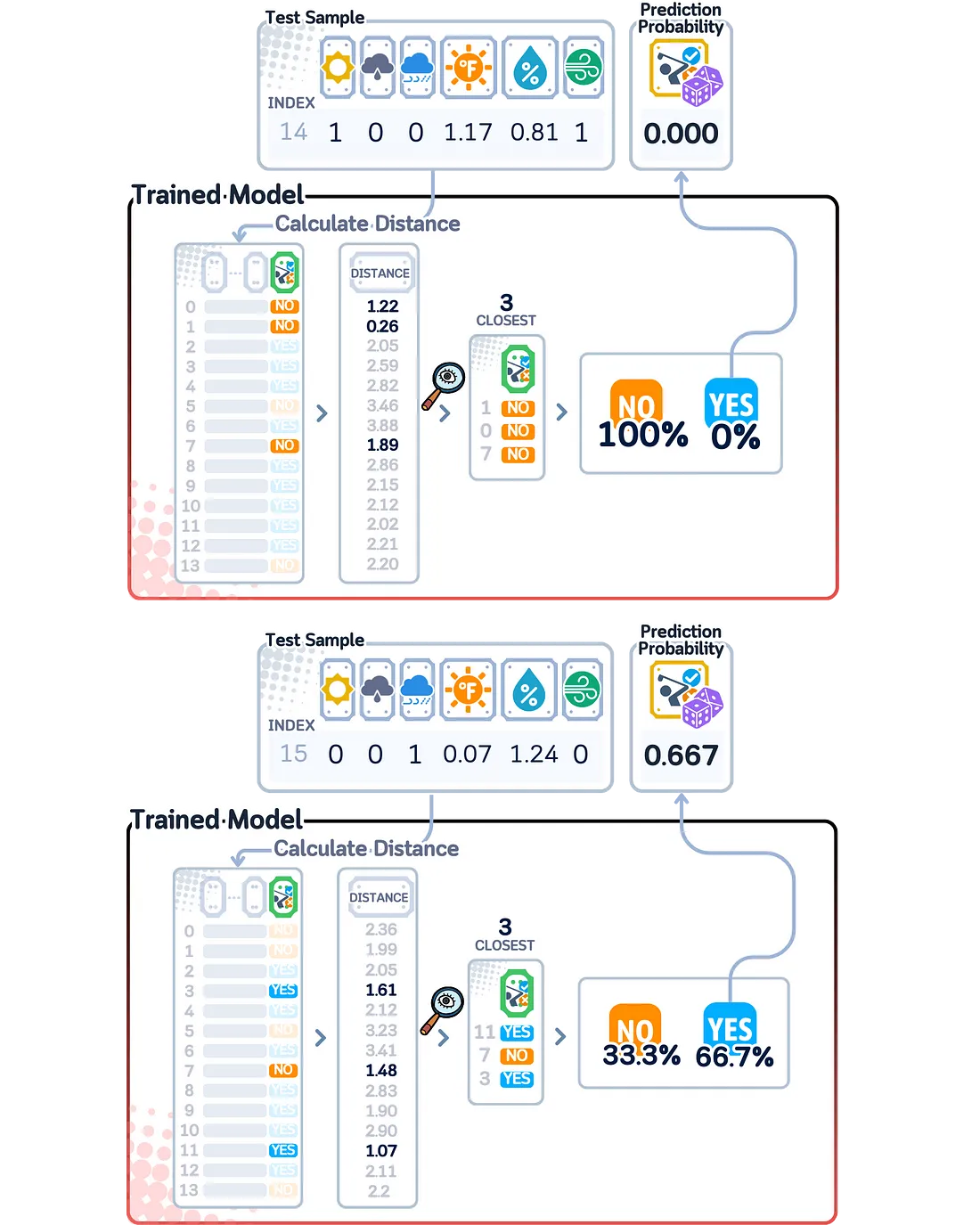
由于kNN通过除法来计算概率得分，因此它只能基于k给出某些特定的值（例如，对于k=5，可能的概率得分只有0/5（0%）、1/5（20%）、2/5（40%）、3/5（60%）、4/5（80%）和5/5（100%））。这意味着kNN无法像其他模型那样提供多种不同的置信度水平。

from sklearn.neighbors import KNeighborsClassifier
import pandas as pd
import numpy as np
# Train the model
k = 3  # number of neighbors
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
# Print the "model"
print("THE MODEL:")
print(f"Number of neighbors (k): {k}")
print(f"Training data points stored: {len(X_train)}")
# Make predictions and get probabilities
y_pred = knn.predict(X_test)
y_prob = knn.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

朴素贝叶斯概率

朴素贝叶斯是一种预测模型，它使用带有“朴素”规则的概率数学：它假设每个特征独立地影响结果。朴素贝叶斯有不同的类型：高斯朴素贝叶斯适用于连续值，而伯努利朴素贝叶斯适用于二值特征。由于我们的数据集有许多0-1特征，因此我们将在这里重点关注伯努利朴素贝叶斯。

当这个模型完成训练后，它会记住概率值：一个值表示正类出现的频率，以及对于每个特征，表示在出现正结果时不同特征值出现的可能性的值。

为了计算预测概率，朴素贝叶斯将几个概率相乘：每个类别出现的概率，以及在该类别中看到每个特征值的概率。然后，将这些相乘的概率进行归一化，使它们的和为1，从而得到最终的概率得分。

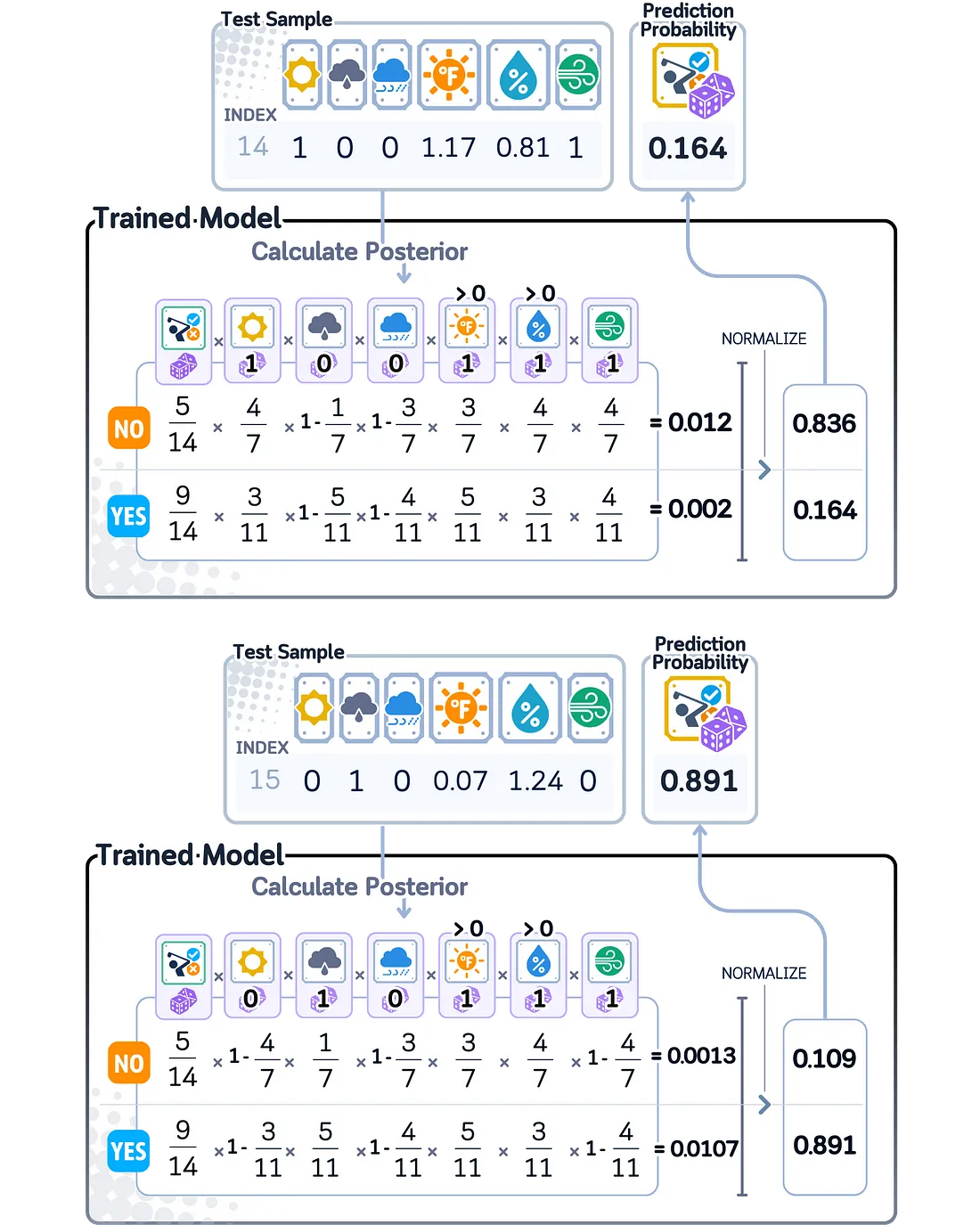
由于朴素贝叶斯使用概率数学，其概率得分自然落在0到1之间。然而，当某些特征强烈指向一个类别而非另一个类别时，该模型可以给出非常接近0或1的概率得分，表明它对预测非常有信心。

from sklearn.naive_bayes import BernoulliNB
import pandas as pd
# Train the model
nb = BernoulliNB()
nb.fit(X_train, y_train)
# Print the "model"
print("THE MODEL:")
df = pd.DataFrame(
   nb.feature_log_prob_.T, 
   columns=['Log Prob (No Play)', 'Log Prob (Play)'], 
   index=['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind']
)
df = df.round(3)
print("\nFeature Log-Probabilities:")
print(df)
print("\nClass Priors:")
priors = pd.Series(nb.class_log_prior_, index=['No Play', 'Play']).round(3)
print(priors)
# Make predictions and get probabilities
y_pred = nb.predict(X_test)
y_prob = nb.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

决策树概率

决策树分类器通过对输入数据创建一系列的是/否问题来工作。它一次构建一个问题，总是选择最有用的、能最好地将数据分成组的问题。它会继续提问，直到在分支的末端得到最终答案。

当这个模型完成训练后，它会创建一棵树，其中的每个点都代表一个关于数据的问题。每个分支显示根据答案应该走的方向，并且每个分支的末端都包含关于训练数据中每个类别出现频率的信息。

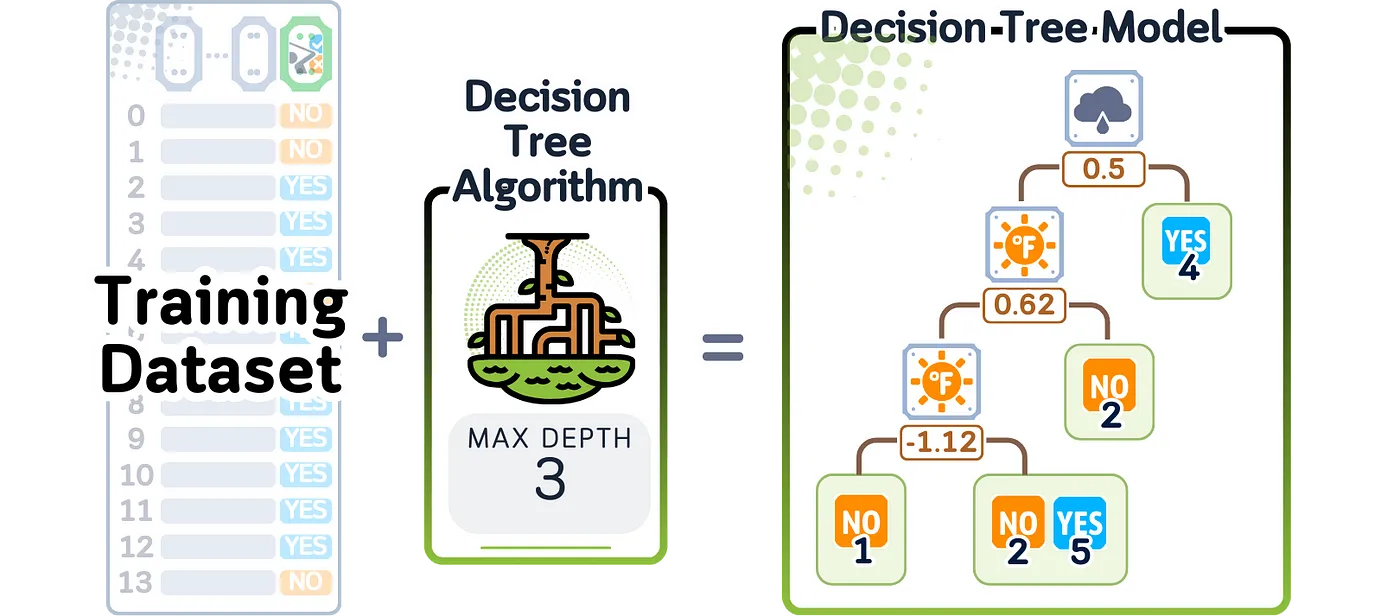
为了计算预测概率，决策树会为新数据依次回答所有问题，直到到达某个分支的末端。概率得分是基于在训练过程中，每个类别的训练样本有多少最终落在了同一个分支上。

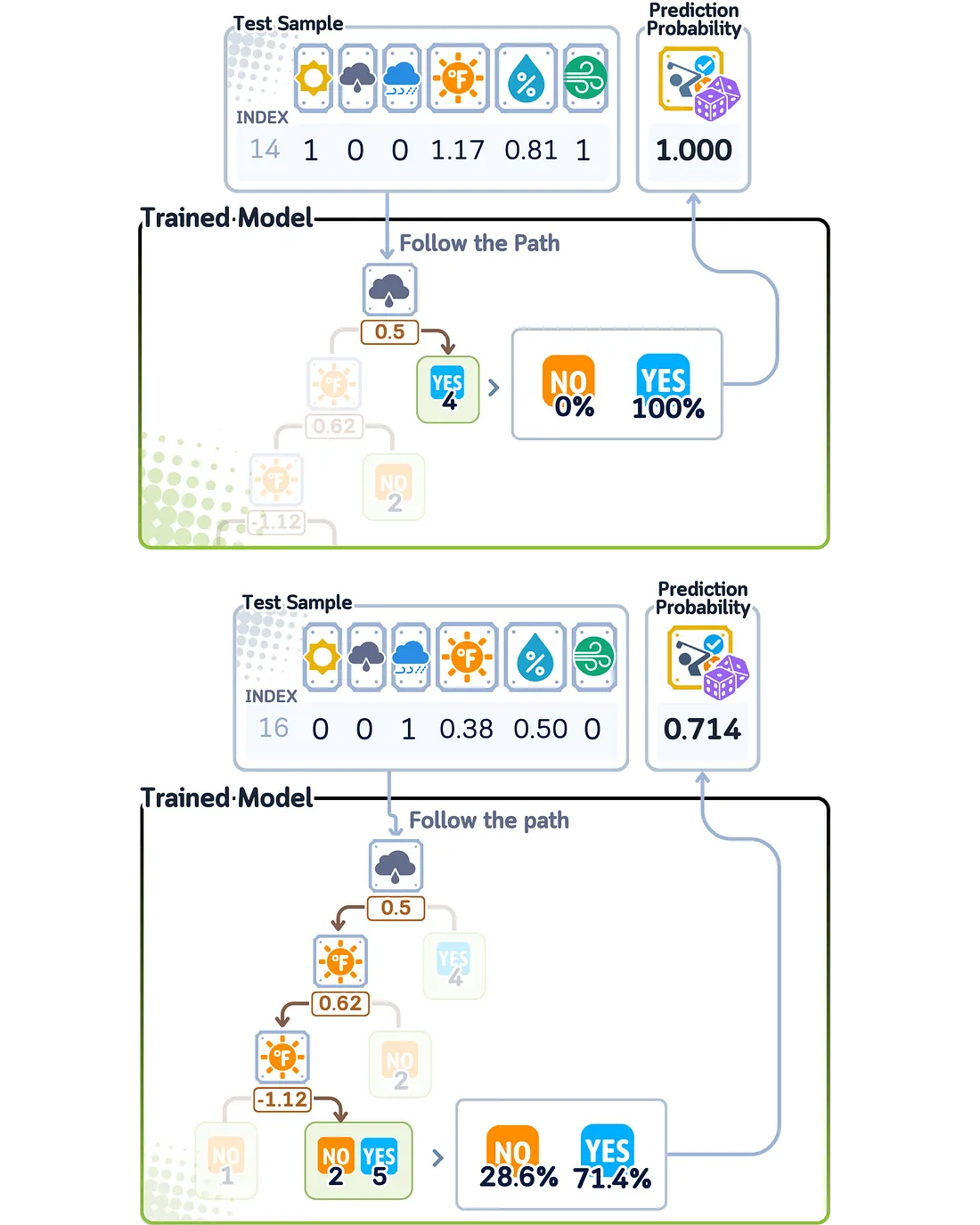
由于决策树的概率得分来自于对每个分支端点训练样本的计数，因此它们只能是训练过程中观察到的某些确定值。这意味着模型只能给出与学习时发现的模式相匹配的概率得分，这限制了其置信度水平的精确程度。

from sklearn.tree import DecisionTreeClassifier, plot_tree
import pandas as pd
import matplotlib.pyplot as plt
# Train the model
dt = DecisionTreeClassifier(random_state=42, max_depth=3)  # limiting depth for visibility
dt.fit(X_train, y_train)
# Print the "model" - visualize the decision tree
print("THE MODEL (DECISION TREE STRUCTURE):")
plt.figure(figsize=(20,10))
plot_tree(dt, feature_names=['sunny', 'overcast', 'rainy', 'Temperature', 
                           'Humidity', 'Wind'], 
         class_names=['No Play', 'Play'],
         filled=True, rounded=True, fontsize=10)
plt.show()
# Make predictions and get probabilities
y_pred = dt.predict(X_test)
y_prob = dt.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

逻辑回归概率

尽管名为回归，但逻辑回归模型实际上是通过一个数学方程来预测两个类别之间的结果。对于输入数据中的每个特征，它会通过赋予一个数字（权重）来学习该特征的重要性。它还会学习一个额外的数字（偏置），以帮助做出更好的预测。为了将这些数字转换成预测概率，它使用了sigmoid函数，该函数将最终结果保持在0到1之间。

当这个模型完成训练后，它所记住的就是这些权重——每个特征对应一个数字，再加上一个偏置数字。这些数字就是它进行预测所需的一切。

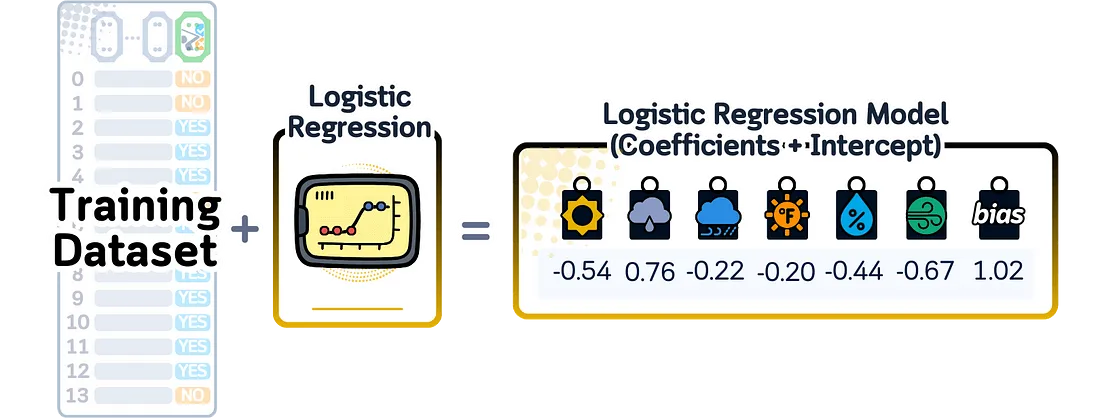
在二分类问题中计算预测概率时，逻辑回归首先会将每个特征值乘以其对应的权重，并将它们全部相加，然后再加上偏置。这个总和可能是任何数字，因此模型会使用sigmoid函数将其转换为0到1之间的概率。

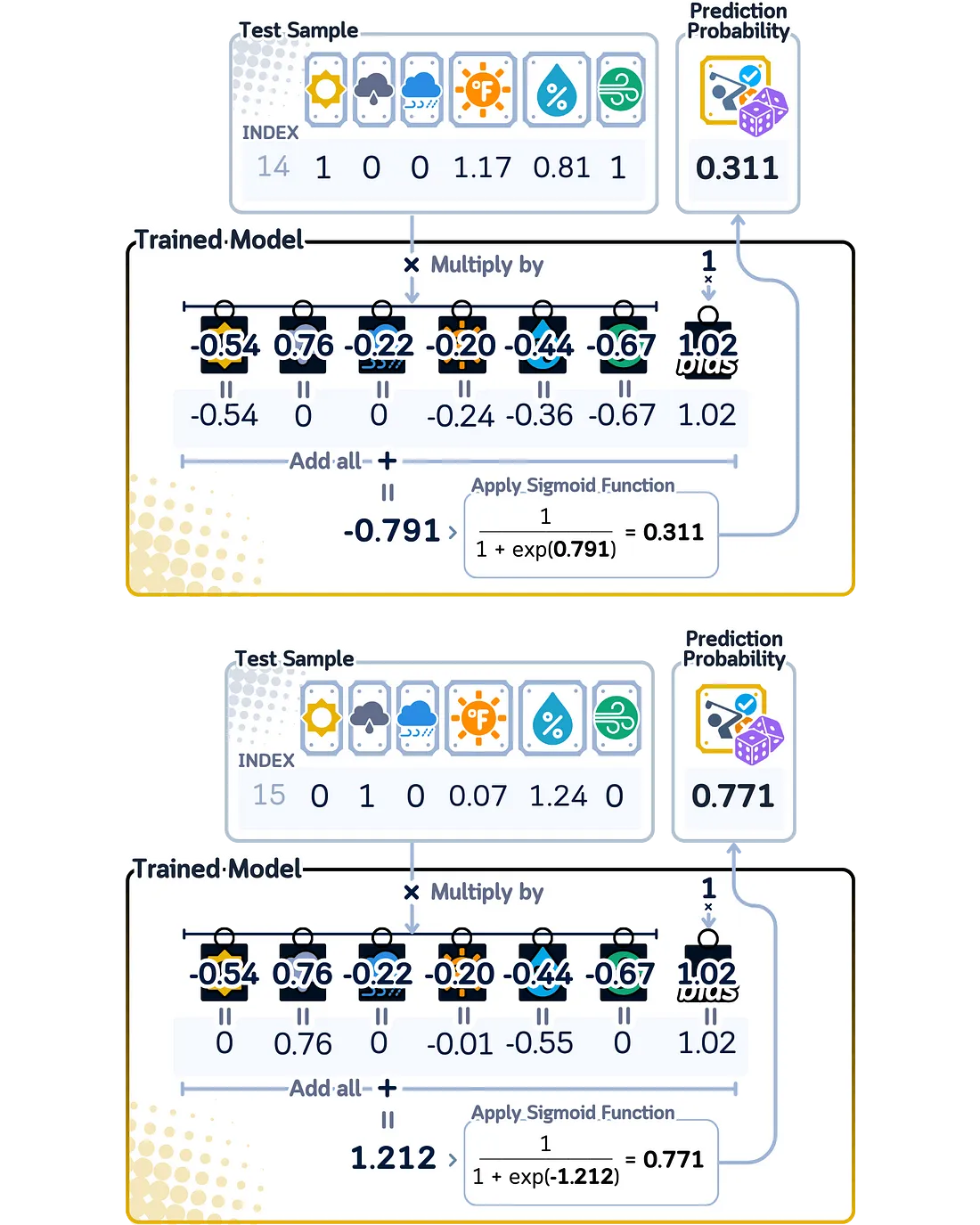
与其他只能给出某些特定概率得分的模型不同，逻辑回归可以给出0到1之间的任何概率。输入数据离模型从一类切换到另一类（即决策边界）的点越远，所得概率就越接近0或1。靠近这个切换点的数据点的概率会更接近0.5，这表明模型对这些预测的置信度较低。

from sklearn.linear_model import LogisticRegression
import pandas as pd
# Train the model
lr = LogisticRegression(random_state=42)
lr.fit(X_train, y_train)
# Print the "model"
print("THE MODEL:")
model_df = pd.DataFrame({
   'Feature': ['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind'],
   'Coefficient': lr.coef_[0]
})
model_df['Coefficient'] = model_df['Coefficient'].round(3)
print("Coefficients (weights):")
print(model_df)
print(f"\nIntercept (bias): {lr.intercept_[0]:.3f}")
print("\nPrediction = sigmoid(intercept + sum(coefficient * feature_value))")
# Make predictions and get probabilities
y_pred = lr.predict(X_test)
y_prob = lr.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

支持向量机（SVM）概率

支持向量机（SVM）分类器的工作原理是找到最佳边界线（或面）来分离不同的类别。它关注离这个边界最近的点（称为支持向量）。虽然基本的SVM找到的是直线边界，但它也可以使用称为核函数的数学函数来创建曲线边界。

当这个模型完成训练后，它会记住三件事：边界附近的重要点（支持向量）、每个点的重要性（权重）以及任何关于曲线边界的设置（核参数）。这些共同定义了边界在哪里以及如何分离类别。

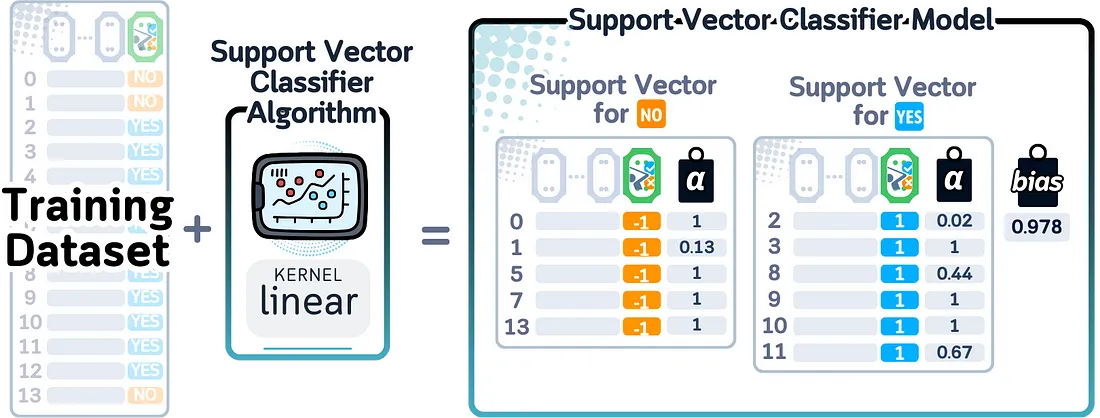
在二分类问题中计算预测概率时，支持向量机（SVM）需要额外的一步，因为它本身并不是为了给出概率得分而设计的。它使用了一种称为Platt缩放的方法，该方法增加了一个逻辑回归层，将距离边界的距离转换为概率。这些距离通过sigmoid函数转换，以得到最终的概率得分。

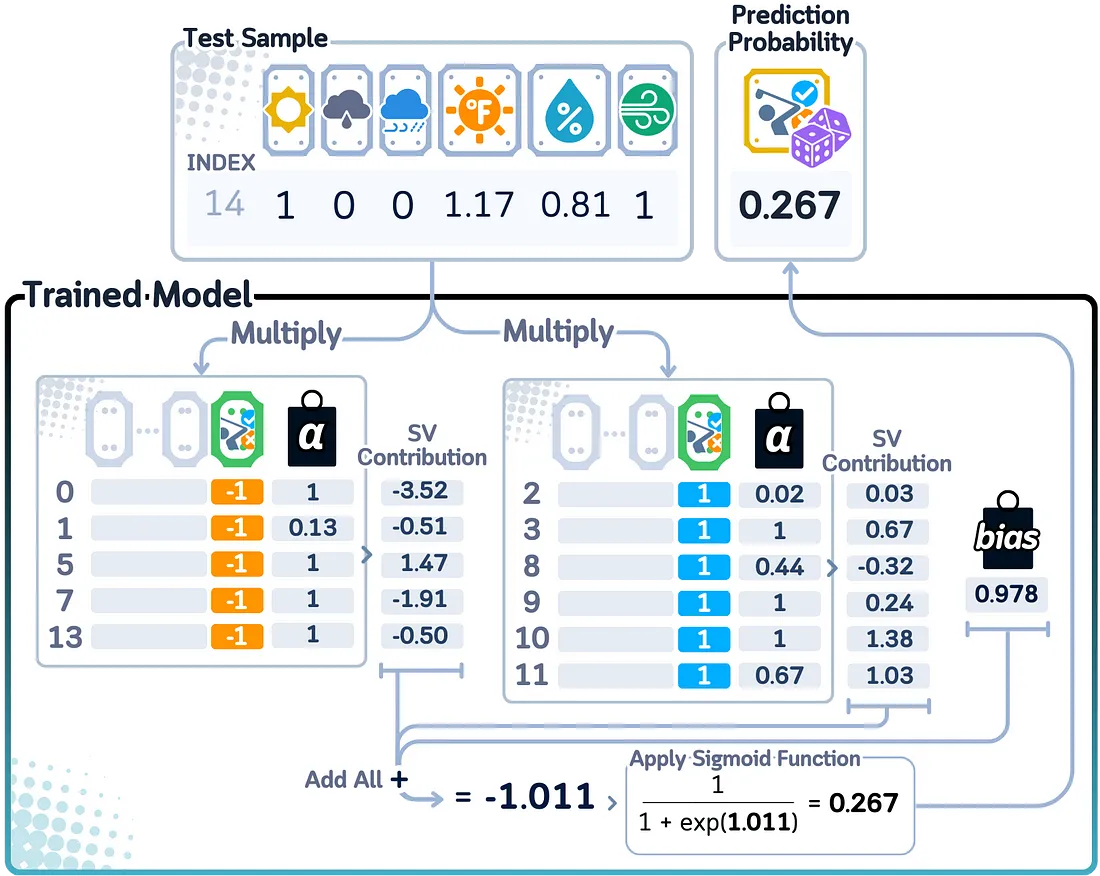
由于SVM以这种间接的方式计算概率，因此得分显示的是点距离边界的远近，而不是真正的置信水平。远离边界的点得到的概率得分更接近0或1，而靠近边界的点得到的得分更接近0.5。这意味着概率得分更多地反映了点相对于边界的位置，而不是模型对其预测的实际置信度。

from sklearn.svm import SVC
import pandas as pd
import numpy as np
# Train the model
svm = SVC(kernel='rbf', probability=True, random_state=42)
svm.fit(X_train, y_train)
# Print the "model"
print("THE MODEL:")
print(f"Kernel: {svm.kernel}")
print(f"Number of support vectors: {svm.n_support_}")
print("\nSupport Vectors (showing first 5 rows):")
# Create dataframe of support vectors
sv_df = pd.DataFrame(
   svm.support_vectors_,
   columns=['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind']
)
print(sv_df.head().round(3))
# Show which classes these support vectors belong to
print("\nSupport vector classes:")
for i, count in enumerate(svm.n_support_):
   print(f"Class {i}: {count} support vectors")
# Make predictions and get probabilities
y_pred = svm.predict(X_test)
y_prob = svm.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

多层感知机概率

多层感知机（MLP）分类器是一种神经网络，它通过多层相互连接的节点（神经元）来处理数据。每个神经元会计算其输入数据的加权总和，然后使用函数（如ReLU）对这个数值进行变换，并将结果发送到下一层。对于二分类问题，最后一层使用sigmoid函数来给出0到1之间的输出。

当这个模型完成训练后，它会记住两件主要的事情：相邻层神经元之间的连接强度（权重和偏置），以及网络的结构（每一层有多少层和神经元）。

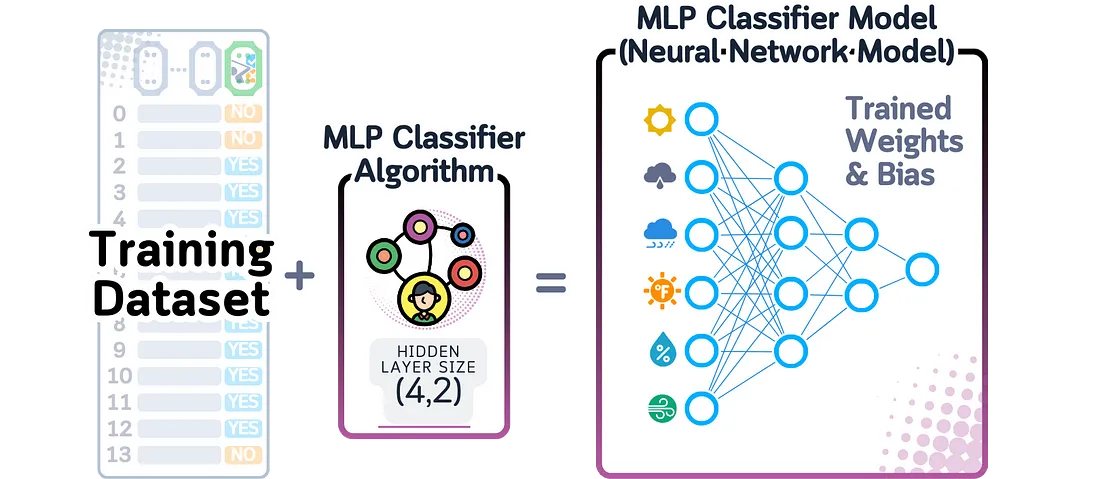
在二分类问题中计算预测概率时，多层感知机（MLP）会将数据通过其各层进行传递，每一层都会从前一层的信息中创建出更复杂的组合。最后一层会生成一个数字，这个数字随后通过sigmoid函数被转换成0到1之间的概率。

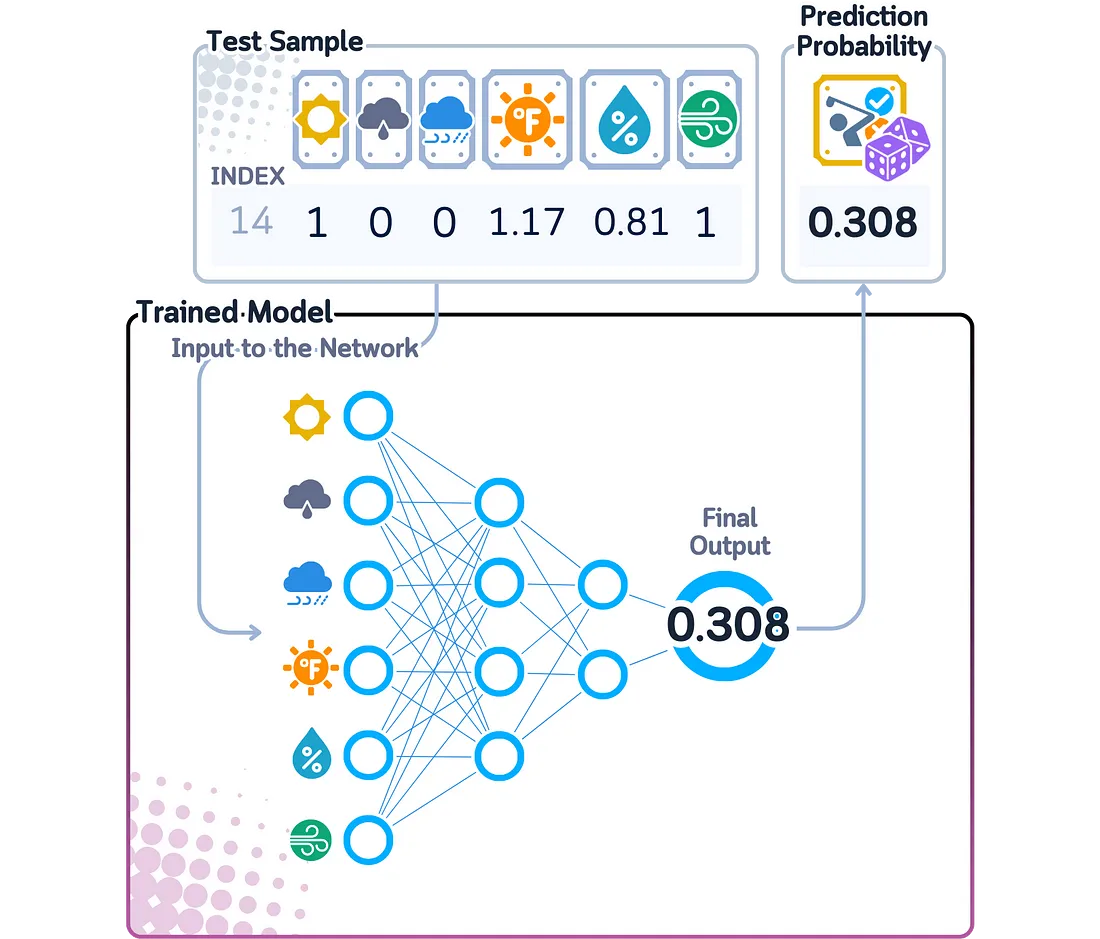
多层感知机（MLP）能够比许多其他模型在数据中发现更复杂的模式，因为它以高级的方式组合特征。最终的概率得分显示了网络的置信度——接近0或1的得分意味着网络对其预测非常自信，而接近0.5的得分则表明它不确定。

from sklearn.neural_network import MLPClassifier
import pandas as pd
import numpy as np
# Train the model with a simple architecture
mlp = MLPClassifier(hidden_layer_sizes=(4,2), random_state=42)
mlp.fit(X_train, y_train)
# Print the "model"
print("THE MODEL:")
print("Network Architecture:")
print(f"Input Layer: {mlp.n_features_in_} neurons (features)")
for i, layer_size in enumerate(mlp.hidden_layer_sizes):
   print(f"Hidden Layer {i+1}: {layer_size} neurons")
print(f"Output Layer: {mlp.n_outputs_} neurons (classes)")
# Show weights for first hidden layer
print("\nWeights from Input to First Hidden Layer:")
weights_df = pd.DataFrame(
   mlp.coefs_[0],
   columns=[f'Hidden_{i+1}' for i in range(mlp.hidden_layer_sizes[0])],
   index=['sunny', 'overcast', 'rainy', 'Temperature', 'Humidity', 'Wind']
)
print(weights_df.round(3))
print("\nNote: Additional weights and biases exist between subsequent layers")
# Make predictions and get probabilities
y_pred = mlp.predict(X_test)
y_prob = mlp.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

模型对比

总结来说，以下是每种分类器如何计算预测概率的方法：

1. 虚拟分类器：基于训练数据中每个类别出现的频率，为所有预测使用相同的概率得分。忽略所有输入特征。
2. K-最近邻：概率得分是属于每个类别的相似邻居的比例。只能基于k值给出特定的比例（如3/5或7/10）。
3. 朴素贝叶斯：将初始类别概率和观察到每个特征值的概率相乘，然后调整结果使它们之和为1。概率得分显示了特征在每个类别中出现的可能性。
4. 决策树：基于最终分支中每个类别出现的频率给出概率得分。只能使用训练期间看到的概率值。
5. 逻辑回归：使用sigmoid函数将加权特征组合转换为概率得分。可以给出0到1之间的任何概率，该概率会根据与决策边界的距离平滑变化。
6. 支持向量机：需要额外一步（Platt缩放）来创建概率得分，使用sigmoid函数将距离边界的距离转换为概率。这些距离决定了模型的置信度。
7. 多层感知机：通过多层变换处理数据，最后以sigmoid函数结束。从复杂的特征组合中创建概率得分，给出0到1之间的任何值。

总结

观察每个模型如何计算其预测概率向我们展示了一个重要的事实：每个模型都有其自己的表示置信度的方式。像虚拟分类器和决策树这样的模型只能基于其训练数据使用某些概率得分。而像逻辑回归和神经网络这样的模型则可以给出0到1之间的任何概率，使它们能够更精确地表达其不确定性。

代码总结

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
# The models
from sklearn.dummy import DummyClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import BernoulliNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
# Load and prepare data
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rainy', 'rainy', 'rainy', 'overcast', 'sunny', 'sunny', 'rainy', 'sunny', 'overcast', 'overcast', 'rainy', 'sunny', 'overcast', 'rainy', 'sunny', 'sunny', 'rainy', 'overcast', 'rainy', 'sunny', 'overcast', 'sunny', 'overcast', 'rainy', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Play': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'Yes']
}
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df['Play'] = (df['Play'] == 'Yes').astype(int)
# Prepare features and target
X,y = df.drop('Play', axis=1), df['Play']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Scale numerical features
scaler = StandardScaler()
X_train[['Temperature', 'Humidity']] = scaler.fit_transform(X_train[['Temperature', 'Humidity']])
X_test[['Temperature', 'Humidity']] = scaler.transform(X_test[['Temperature', 'Humidity']])
# Train the model
clf = DummyClassifier(strategy='stratified', random_state=42)
# clf = KNeighborsClassifier(n_neighbors=3)
# clf = BernoulliNB()
# clf = DecisionTreeClassifier(random_state=42, max_depth=3)
# clf = LogisticRegression(random_state=42)
# clf = SVC(kernel='rbf', probability=True, random_state=42)
# clf = MLPClassifier(hidden_layer_sizes=(4,2), random_state=42)
# Fit and predict
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
y_prob = clf.predict_proba(X_test)
# Create results dataframe
results_df = pd.DataFrame({
   'True Label': y_test,
   'Prediction': y_pred,
   'Probability of Play': y_prob[:, 1]
})
print("\nPrediction Results:")
print(results_df)
# Print accuracy
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")