数学推理已成为人工智能领域中的一大关键前沿，特别是在开发能够执行复杂问题解决任务的大型语言模型（LLMs）方面。传统上，数学推理主要依赖于基于文本的输入，但现代应用已越来越多地融入了多模态元素，如图表、图形和公式。这一趋势对现有系统在处理和整合不同模态信息方面提出了严峻挑战。这些挑战不仅涉及简单的文本理解，还包括深层语义理解、跨模态上下文保持能力，以及结合视觉和文本元素进行复杂推理的能力。

自2021年以来，针对数学的大型语言模型（MathLLMs）数量稳步增长，每个模型都在解决数学问题的不同方面展现出了独特的能力。早期的模型如GPT-f和Minerva奠定了数学推理的基础，而Hypertree Proof Search和九章1.0则在定理证明和问题理解上取得了显著进展。到了2023年，通过像SkyworkMath这样的模型，多模态支持被引入，进一步丰富了数学推理的应用场景。2024年，则专注于数学教学（如Qwen2.5-Math）和证明能力（如DeepSeek-Proof）的专门发展。

尽管取得了这些进步，现有的方法仍过于专注于特定数学领域，或未能充分解决多模态数学推理的挑战。为了深入理解这一领域的发展格局，来自香港科技大学（广州）、香港科技大学、南洋理工大学和松鼠AI的研究人员提出了全面的分析框架。他们审阅了自2021年以来发表的200多篇研究论文，聚焦于Math-LLMs在多模态环境中的出现和演变。

该框架考察了多模态数学推理流程，同时对比了传统LLMs和MLLMs（多模态大型语言模型）的作用。研究特别强调了影响在数学推理中实现人工通用智能的五大主要挑战：视觉推理限制、限制的多模态整合、领域泛化问题、错误检测与反馈机制缺乏，以及教育整合挑战。

在问题解决场景中，输入可能由纯文本格式的问题陈述或伴随图形和图表的视觉元素组成。系统需要处理这些输入，并生成数值或符号格式的解决方案。尽管英语在现有基准中占主导地位，但仍有一些数据集以其他语言存在，如中文和罗马尼亚语。数据集的大小差异显著，从小型集合如QRData（包含411个问题）到大型库如OpenMathInstruct-1（包含180万对问题解决方案）不等。

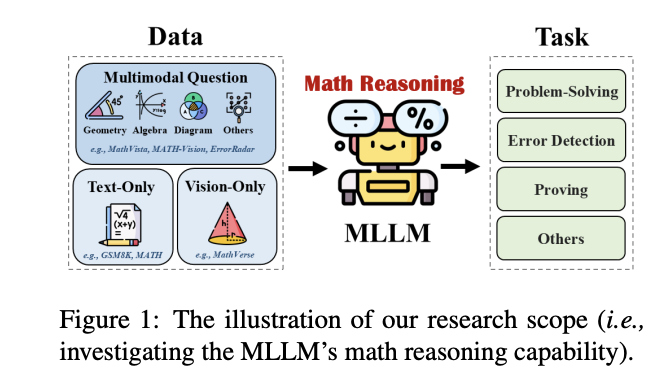
对MLLMs中数学推理能力的评估主要采用两种方法：判别性评估方法和生成性评估方法。判别性评估方法侧重于模型正确分类或选择答案的能力，采用高级指标如性能下降率（PDR）和专门指标如错误步骤准确性。而生成性评估方法则关注模型产生详细解释和步骤解决方案的能力。值得注意的框架如MathVerse利用GPT-4评估推理过程，而CHAMP则实施了解决方案评估流程，其中GPT-4作为阅卷者，将生成的答案与标准答案进行比较。

综上所述，研究人员对MLLMs中的数学推理进行了全面深入的分析，揭示了该领域的显著进展和持续存在的挑战。Math-LLMs的出现展示了在处理复杂数学任务方面的重大进展，特别是在多模态环境中。然而，要解决以上五个关键挑战，开发能够进行类人数学推理的更复杂AI系统仍然至关重要。该分析提供的见解为未来研究方向提供了路线图，强调了需要更多健壮、多功能的模型来有效应对数学推理的复杂性。