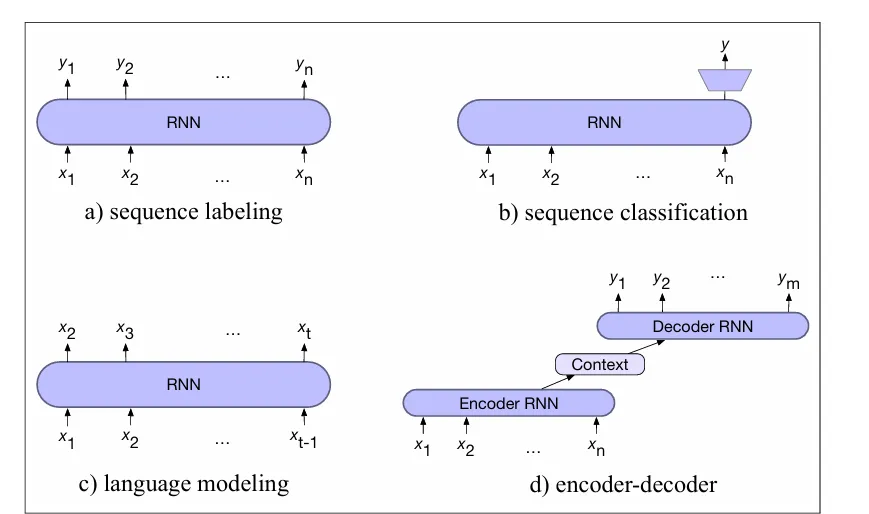
Transformer核心架构:编码器-解码器模型
当我们需要将一个输入序列转换为一个与输入序列不是逐字对齐且长度可变的输出序列时,就会采用Encoder-Decoder模型。请记住,每个输入都与一个特定的输出相关联,输出的标注主要使用局部信息,并且在序列标注任务中,两个序列的长度是相同的(例如,在词性标注中,每个词都会获得一个相关的标签)。因此,在判断一个词是动词还是名词时,我们主要考虑该词及其周围的词。然而,输入中的一个词与输出中的一个词之间的映射可能是非常间接的(在某些语言中,动词出现在句子的开头,而在其他语言中则出现在句尾),Encoder-Decoder模型特别适用于像机器翻译这样的任务,在这些任务中,输入和输出序列的长度可能不同。
给定一个输入序列,编码器-解码器网络(也称为序列到序列网络)是能够生成与上下文相关的任意长度输出序列的模型。尽管编码器-解码器网络已被用于多种任务,如对话、问题回答和摘要生成,但它们最常用于机器翻译。这些网络的基本概念是使用编码器网络接收输入序列并生成其上下文表示(通常称为上下文)。然后,解码器接收这个表示并生成针对特定任务的输出序列。
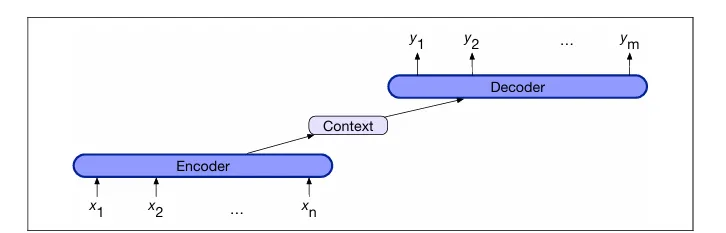
编码器-解码器网络有三个概念部分:
1. 编码器,它从输入序列x1:n创建一系列上下文表示h1:n。编码器可以是Transformer、LSTM或卷积网络。
2. 上下文向量c,它是h1:n的函数,为解码器提供输入的主要信息。
3. 解码器接收c作为输入,并产生任意长度的隐藏状态序列h1:m,从而获得可比较的输出状态序列y1:m。与编码器类似,任何类型的序列架构都可以用来构建解码器。
我们从条件RNN语言模型p(y)开始,它表示序列y的可能性,然后构建编码器-解码器模型的方程。记住,在任何语言模型中,我们都可以根据概率的链式规则将概率分解为:
p(y) = p(y1)p(y2|y1)p(y3|y1,y2)...p(ym|y1,...,ym-1)
在RNN语言建模中,在特定时间t,将t-1个词的前缀送入语言模型。然后,使用前向推断生成一系列隐藏状态,其中最后一个隐藏状态对应于前缀的最后一个词。接下来,以前缀的最终隐藏状态为起点,生成下一个词。
正式来说,如果在时间t,g是一个激活函数(如tanh或ReLU),是时间t的输入和时间t-1的隐藏状态的函数,并且softmax是在潜在词汇项集合上进行的,那么时间t的输出yt和隐藏状态ht计算如下:
ht = g(ht-1, xt)
yt = softmax(ht)
为了将这个具有自回归生成的语言模型转变为编码器-解码器模型(即将一种语言的源文本转换为另一种语言的目标文本的翻译模型),我们只需要做一个小调整:
在源文本末尾添加句子分隔符后,将目标文本连接起来。让我们以句子分隔符标记为例,将英文源文本(“the green witch arrived”)转换为西班牙语句子(“llegó la bruja verde”,可以逐字解释为“arrived the witch green”)。我们也可以使用问答对或文本摘要对来演示编码器-解码器概念。
让我们用y来指代目标文本y(在此示例中为西班牙语),用x来指代带有分隔符符号的源文本(在此例中为英语)。然后,编码器-解码器模型以下述方式计算概率p(y|x)。
p(y|x) = p(y1|x)p(y2|y1,x)p(y3|y1, y2, x)...p(ym|y1,...,ym-1,x)
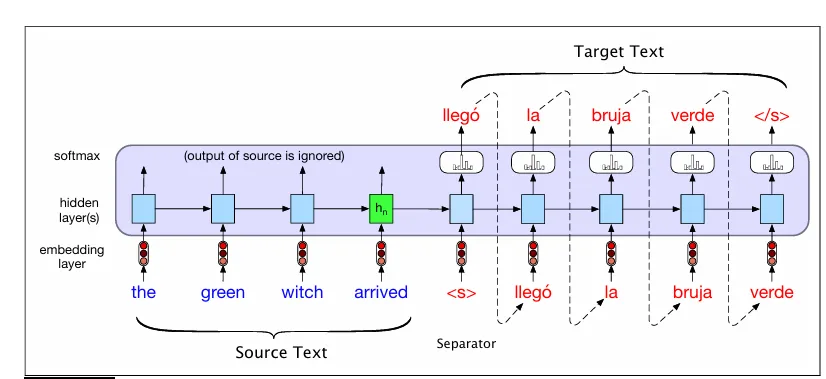
该图展示了简化版的编码器-解码器模型的设置,并显示了西班牙语目标文本(“llegó la bruja verde”)、英语源文本(“the green witch arrived”)以及句子分隔符标记()。通过前向推断将源文本传入网络进行翻译,网络会生成隐藏状态,直到源文本处理完毕。接下来,我们开始自回归生成,在隐藏层的上下文中,从源输入的末尾和句子结束标记处请求一个词。生成的最后一个词的嵌入和之前的隐藏状态作为后续词的条件。为了保持一致,我们将在必要时使用上标e和d来区分编码器和解码器的隐藏状态。让我们对这个模型进行形式化和泛化。
编码器由左侧的网络组件组成,这些组件处理输入序列x。编码器由堆叠的双向LSTM(biLSTM)组成,其中前向和后向传递的顶层隐藏状态被连接起来,以为每个时间步提供上下文表示。尽管我们的简化图仅为编码器描绘了一层网络,但堆叠架构是常态,堆叠顶层的输出状态被视为最终表示。
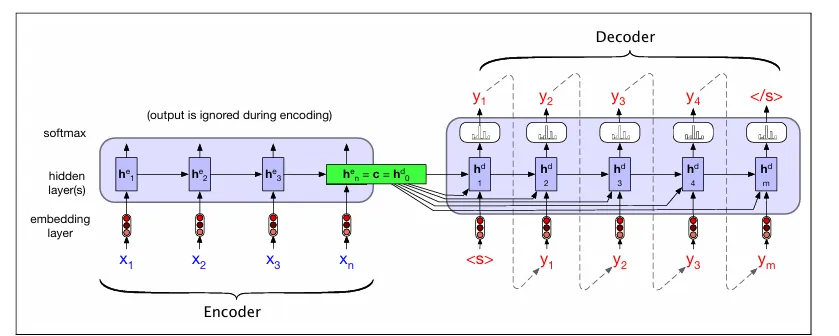
创建输入的上下文表示是编码器的唯一目标。编码器的最终隐藏状态h_n就是这种表示的体现。然后,将这个表示(也称为上下文c)提供给解码器。第一个解码器RNN单元将使用c作为其先前的隐藏状态h_d^0,而解码器网络的最基本版本将仅使用这个状态来初始化解码器的第一个隐藏状态。然后,解码器将以自回归的方式逐个元素地生成一系列输出,直到生成序列结束标记。每个隐藏状态都依赖于前一个状态生成的输出以及先前的隐藏状态。
如图所示,我们采用了一种更复杂的方法:我们使上下文向量c对除初始解码器隐藏状态以外的其他状态也可访问,以确保在生成输出序列时,上下文向量的影响不会减弱。我们通过将c作为当前隐藏状态计算中的一个参数来实现这一点,使用以下方程:
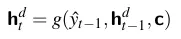
在每个解码时间步都提供上下文的情况下,我们现在可以查看基本编码器-解码器模型中此版本解码器的完整方程。请记住,ˆy_{t-1}是前一阶段从softmax中采样得到的输出的嵌入,而g代表特定类型的RNN:
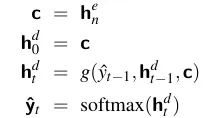
因此,y_t是词汇表上的一个概率向量,表示每个词在时刻t出现的可能性。我们从这个分布y_t中采样以生成文本。在每个时间步简单地选择最有可能生成的词就是一个贪婪决策的例子。
注意力机制
编码器-解码器模型的简洁之处在于其将编码器(创建源文本的表示)和解码器(使用这个上下文创建目标文本)明确分开。到目前为止,在我们所解释的模型中,这个上下文向量是h_n,即源文本最后一个(第n个)时间步的隐藏状态。
因此,这个最后的隐藏状态起到了瓶颈的作用,因为解码器仅知道这个上下文向量中包含的内容,所以它必须表示源文本意义的各个方面。特别是对于长句子,句子开头的信息可能不会在上下文向量中得到清晰反映。

通过使解码器能够从编码器的所有隐藏状态(而不仅仅是最近的一个)中获取信息,注意力机制解决了瓶颈问题。在注意力机制中,上下文向量c是一个单一向量,它依赖于编码器的隐藏状态,即c = f(h_1e),这与基本的编码器-解码器范式非常相似。由于隐藏状态的数量会随着输入的大小而变化,因此我们无法直接使用完整的编码器隐藏状态向量集作为解码器的上下文。
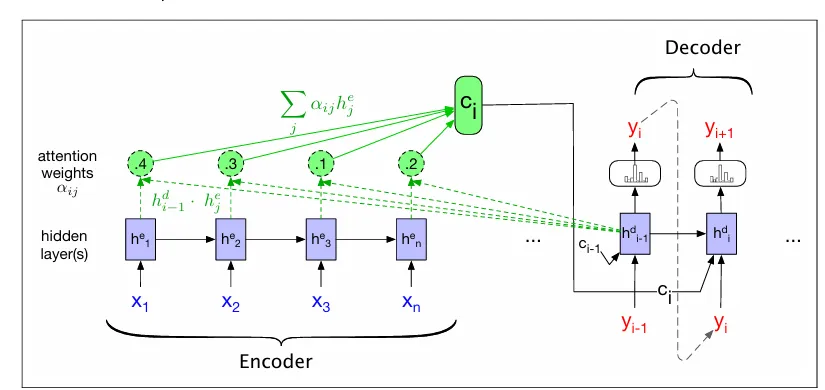
相反,注意力机制的概念是取所有编码器隐藏状态的加权总和,并用它来构建一个单一的固定长度向量c。权重的关注点在于源文本中与解码器当前正在生成的标记相关的特定部分。因此,注意力机制用一个动态上下文向量(在解码过程中的每个标记都会变化)来替代,这个向量是从编码器的隐藏状态中派生出来的。在解码的每一步I中,都会生成一个新的上下文向量c_i,并且其派生过程会考虑到每一个编码器的隐藏状态。这个架构和方程展示了我们如何以这个上下文为条件来计算当前解码器的隐藏状态(同时考虑先前的隐藏状态和解码器生成的前一个输出),以便在解码过程中使用这个上下文:
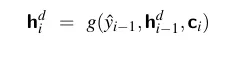
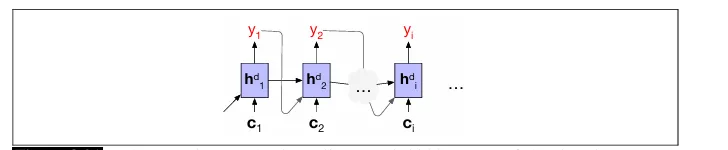
计算应该对每个编码器状态给予多少注意力,以及每个编码器状态与记录在h_i-1^d中的解码器状态的相关性,是计算c_i的第一步。为了在解码过程中捕捉相关性,我们在解码的每个状态i时,为每个编码器状态j确定一个分数(h_i-1^d, h_j^e)。这些分数中最基本的一种称为点积注意力,它通过计算编码器隐藏状态和解码器隐藏状态之间的点积来确定它们的相似度,从而将相关性作为相似度来使用:
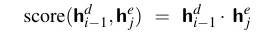
这个点积产生一个分数,这是一个标量,表示两个向量的相似程度。这个分数向量涵盖了所有编码器隐藏状态,提供了每个编码器状态对当前解码器步骤的重要性。
这些分数将通过softmax进行归一化,以产生一个权重向量a_ij,该向量表示每个编码器隐藏状态j对于前一个解码器隐藏状态h_i-1^d的相对重要性。
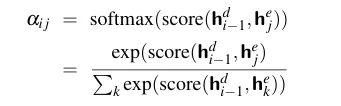
最后,通过对所有编码器隐藏状态进行加权平均,我们可以根据给定的分布,为当前的解码器状态计算出一个固定长度的上下文向量。
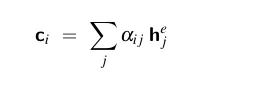
因此,我们最终得到了一个固定长度的上下文向量,它考虑了来自完整编码器状态的数据,并且这个向量会动态调整,以在解码过程的每个阶段都代表解码器的需求。底部的图像展示了一个注意力集中的编码器-解码器网络,它计算出一个单一的上下文向量ci。
也可以为注意力模型开发更复杂的评分函数。通过为评分函数配备其自身的一组权重Ws进行参数化,我们可以获得一个更强大的函数,该函数能够计算每个编码器隐藏状态与解码器隐藏状态之间的相关性,而不仅仅是使用点积注意力。
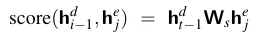
得益于权重Ws,网络可以学习到编码器和解码器状态之间哪些相似性特征对当前应用来说是重要的,随后通过标准的端到端训练对这些权重进行教学。与简单的点积注意力不同,点积注意力要求编码器和解码器的隐藏状态具有相同的维度,而这种双线性模型允许编码器和解码器使用不同维度的向量。































