在本文中，我们将探讨缩放点积注意力机制（通常称为自注意力机制）及其在 Transformer 架构中的关键作用。本文将深入解释数学基础并通过代码示例展示其实现。

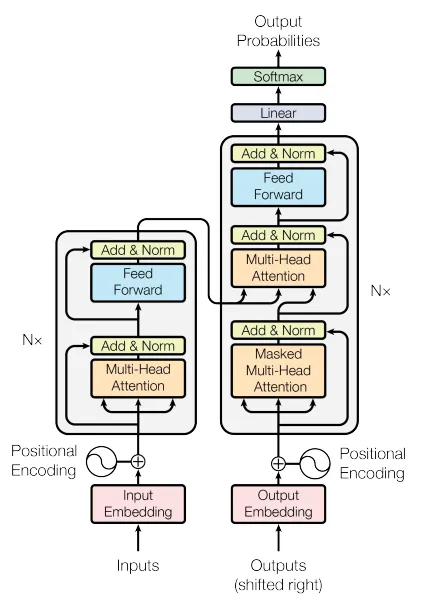
Transformers 中使用了两种主要的注意力机制，主要是多头注意力机制和 Masked Multi-Head Attention，它们在下面的架构图中分别由指针 1、2 和 3 表示。

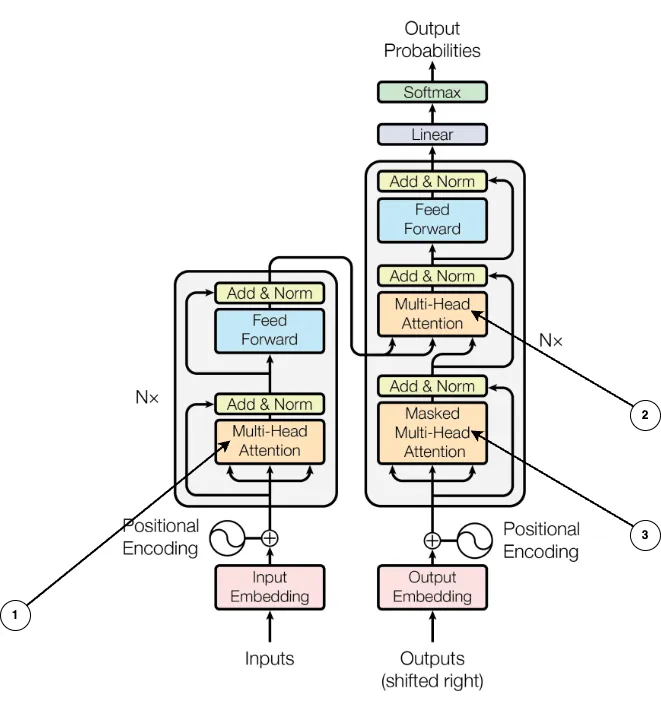
为了理解多头注意力（Multi-Head Attention）和掩码多头注意力（Masked Multi-Head Attention），我们首先需要了解什么是缩放点积注意力（Scaled dot product attention），它也被称为自注意力机制，而其他注意力机制都是这一方法的扩展。

为什么需要注意力机制？

循环神经网络（RNN），包括其高级变体如长短期记忆（LSTM）网络和门控循环单元（GRU），长期以来一直被认为是处理序列到序列学习任务（如语言建模和机器翻译）的领先技术。随着时间的推移，研究人员不断改进这些循环语言模型和编码器-解码器框架，以提高其性能和功能。

在循环模型中，计算是按顺序结构化的，对应于输入和输出序列中符号的位置。每一步都基于前一个隐藏状态h(t-1)和当前位置t的输入生成一个隐藏状态h(t)。然而，这种逐步依赖关系本质上限制了训练过程中的并行化。随着序列变长，这种顺序性质会带来挑战，因为内存限制使得难以高效地批量处理多个示例。

为了解决LSTM、GRU以及其他序列到序列的编码器-解码器架构中存在的问题，引入了注意力机制。换句话说，注意力机制（以下我们将称之为自注意力）会更加重视上下文，并根据元素的重要性和关系动态地调整它们。

想象一下，你正在图书馆里找一本特定的书。你向图书管理员描述这本书（你的查询）。图书管理员了解不同的书籍（键）及其内容（值）。根据你的描述与每本书的描述（兼容性）匹配的程度，图书管理员会挑选出最相关的书籍，并给你它们的摘要（加权输出）。

缩放点积注意力或自注意力的实现

我们开始通过建立一个从单词到索引的离散映射，这个映射称为字典。在我们的例子中，字典被故意保持得很短，但一般来说，这些词汇表的大小会达到大约50,000个词。

import torch
import torch.nn.functional as F
dictionary = {
    "I": 1,
    "Like": 2,
    "AI": 3,
    "And": 4,
    "Machine": 5,
    "Learning": 6,
    "Data": 7,
    "Model": 8,
    "Code": 9,
    "Algorithms": 10,
    "Python": 11,
    "Research": 12,
    "Robots": 13,
    "Deep": 14,
    "Networks": 15,
    "Compute": 16,
    "Vision": 17,
    "Tools": 18,
    "Projects": 19,
    "Neural": 20,
    "Knowledge": 21,
    "Automation": 22,
    "Innovation": 23
}

这实现了一个双射函数 f : W → {1, . . . , |V|}，其中 W 是我们的词汇空间，|V| = 23 是词汇表的大小。嵌入层将离散的单词索引转换为连续的向量表示。

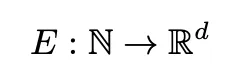
sentence = "I Like Machine Learning And Deep Learning""I Like Machine Learning And Deep Learning"
tensor = torch.tensor([dictionary[s] for s in sentence.split(" ")])
print(f"sentence as a tensor: {tensor}")

输出如下所示。

sentence as a tensor: tensor([ 1,  2,  5,  6,  4, 14,  6])

vocab_size = len(dictionary)  # max value is 23len(dictionary)  # max value is 23
embedding_dim = 4
torch.manual_seed(12)
model = torch.nn.Embedding(vocab_size, embedding_dim)
embedded_tensor = model(tensor).detach()
X = embedded_tensor
# print(embedded_tensor)
print(f"shape of embedded tensor: {embedded_tensor.shape}")
print(f"sequence length: {embedded_tensor.shape[0]} tokens")
print(f"dimension (d) of each token: {embedded_tensor.shape[1]}")

输出如下所示。

shape of embedded tensor: torch.Size([7, 4])
sequence length: 7 tokens
dimension (d) of each token: 4

自注意力机制从输入嵌入的三个线性投影开始。主要的假设是总是选择 d_k < d。在我们的例子中，我们选择 d_k 为 3。

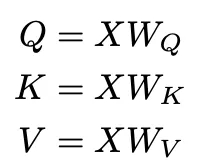
# define the hyper parameters like query, key and value dimensions d(k) d(q) and d(v)as 3
d_k = d_q = d_v = 3
d = 4
# Random weight matrices (embedding size = 4, projected size = 3)
W_q = torch.randn(d, d_q)  # For queries
W_k = torch.randn(d, d_k)  # For keys
W_v = torch.randn(d, d_v)  # For values
# Compute Q, K, V matrices
Q = torch.matmul(X, W_q)  # Shape: (7, 3)
K = torch.matmul(X, W_k)  # Shape: (7, 3)
V = torch.matmul(X, W_v)  # Shape: (7, 3)
# Print results
# Weight Matrices:
# W_q, W_k, W_v: Shape (4, 3)
# - These are the learned projection matrices that transform the input embeddings
#   from the original dimension (4) to the projected dimension (3) for queries, keys, and values.
# Projected Matrices:
# Q, K, V: Shape (7, 3)
# - Q, K, V are the resulting matrices after projecting the input embeddings.
# - 7: Number of tokens in the input sequence.
# - 3: Dimension of each token in the projected space.
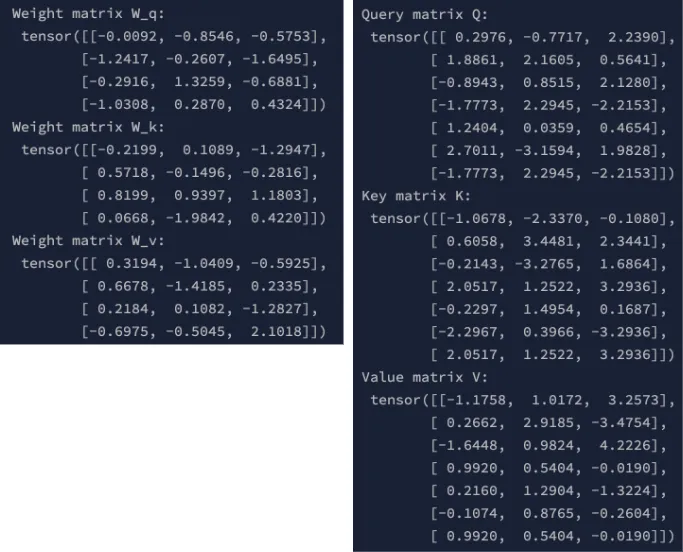
print("Weight matrix W_q:\n", W_q)
print("Weight matrix W_k:\n", W_k)
print("Weight matrix W_v:\n", W_v)
print("Query matrix Q:\n", Q)
print("Key matrix K:\n", K)
print("Value matrix V:\n", V)

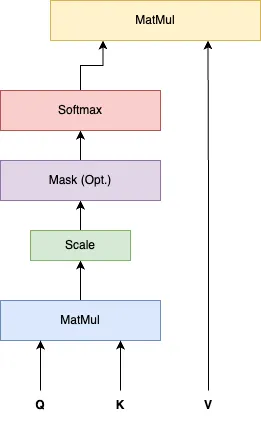
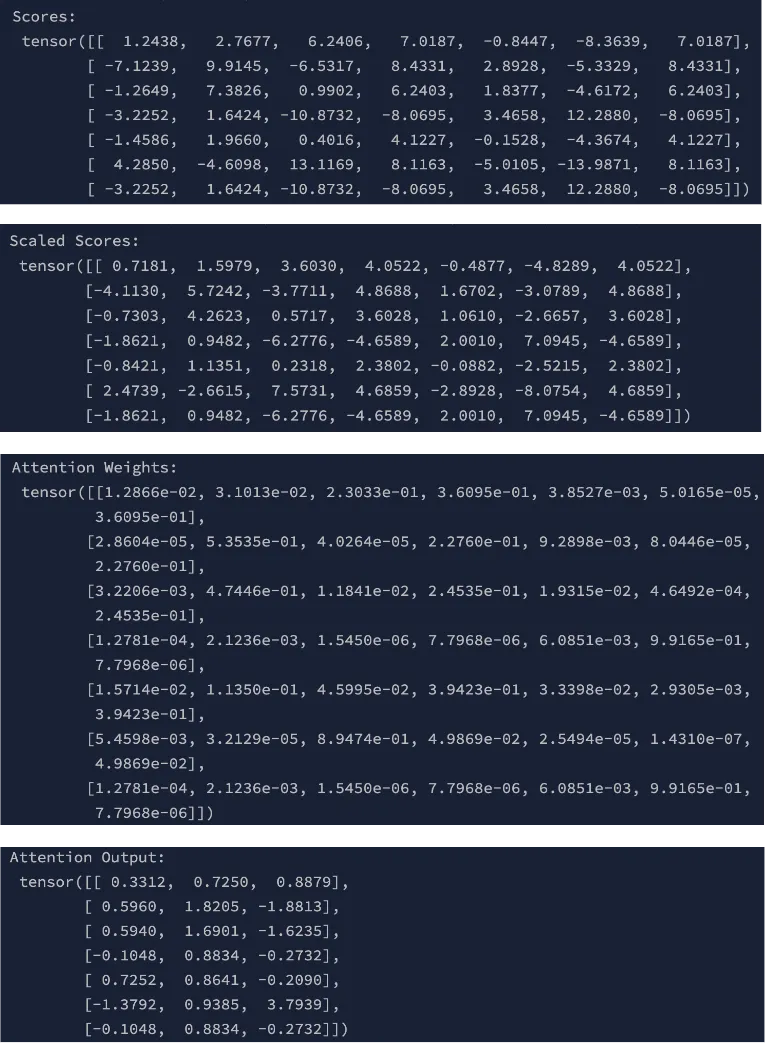
让我们从计算输入数据中查询向量（Q）与每个键向量（K）之间的相似度得分开始。这是通过点积运算实现的，该运算衡量查询向量和键向量的对齐程度或相似度。这些得分表示每个键相对于查询应获得的注意力程度。

为了防止得分过大，从而可能使训练过程不稳定，我们对得分进行缩放。具体做法是将得分除以查询/键向量大小（d_k）的平方根。这一缩放步骤确保值保持在合理范围内，使计算更加稳定。

缩放后，使用softmax函数将得分转换为概率。softmax对缩放后的得分进行归一化，将其转换为总和为1的值。这些概率代表注意力权重，即相对于查询为每个键分配的重要程度。

最后，计算注意力输出。这是通过将注意力权重与值向量（V）相乘实现的。结果是一个值的加权组合，其中权重由注意力机制确定。此输出反映了模型基于计算出的注意力权重对输入数据中最相关部分的关注。

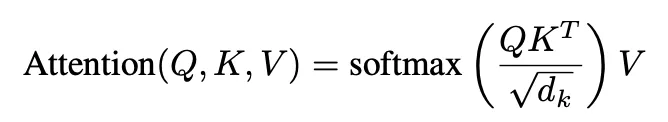
# Compute Attention Scores
"""
The attention scores are computed using the dot product between the query (Q) and key (K) 
vectors for each token. This gives a score that measures the similarity between each query and key.
"""
scores = torch.matmul(Q, K.transpose(-2, -1))
# Scale the Scores
"""
To prevent large values (which can destabilize training), 
scale the scores by the square root of the query/key dimension
"""
d_k = Q.size(-1)  # Query/key dimension (3 in this case)
scaled_scores = scores / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))
# Apply Softmax
# The scaled scores are passed through a softmax function to normalize them into probabilities (attention weights):
# Attention Weights = softmax( Scaled Scores)
attention_weights = F.softmax(scaled_scores, dim=-1)  # Shape: (7, 7)
# Compute Attention Output
# The attention output is computed by multiplying the attention weights with the value (V) matrix:
# Attention Output=Attention Weights⋅V
attention_output = torch.matmul(attention_weights, V)  # Shape: (7, 3)
# Print results
print("Scores:\n", scores)
print("Scaled Scores:\n", scaled_scores)
print("Attention Weights:\n", attention_weights)
print("Attention Output:\n", attention_output)

结论

在本文中，我们探讨了缩放点积注意力机制，也称为自注意力机制，它是Transformer架构的核心。我们首先定义了注意力的关键组件——查询、键和值，并研究了它们在数学上如何相互作用以确定序列中每个标记的重要性。

通过实际实现，我们展示了如何将标记转换为连续嵌入，然后使用可学习的权重矩阵将其投影到Q、K和V矩阵中。我们使用点积计算相似度得分，为了稳定性对这些得分进行缩放，并使用softmax函数对其进行归一化以得出注意力权重。然后，这些权重被用于计算值的加权组合，从而产生最终的注意力输出。

自注意力机制使模型能够动态地关注输入序列的不同部分，并根据上下文分配重要性。这种高效且并行处理长距离依赖的能力使其成为传统序列模型（如RNN和LSTM）的优越替代方案。

通过理解这一核心机制，我们为进一步探索更高级的注意力形式奠定了基础，如多头注意力、掩码多头注意力和多头交叉注意力，这些机制扩展了这些原理，以在机器翻译和语言建模等应用中实现更好的性能。本文搭建了从理论概念到实际实现的桥梁，提供了对注意力机制在现代深度学习模型中至关重要的深刻理解。