神经网络中的神经元执行的是线性操作：它们将输入向量与权重向量相乘，然后加上一个偏置——这些都是线性操作。

因此，如果没有激活函数，它们无法学习非线性数据中的模式。这些激活函数接收神经元的输出，将线性数据映射到非线性范围，从而为整个系统引入了学习非线性数据所需的非线性。因此，激活函数也被称为“非线性函数”并不奇怪，尽管严格来说，f(x) = x 也可以是一个激活函数。

在这篇文章中，我们将概述激活函数，以及一些将在未来文章中更详细介绍的激活函数。这可以帮助你快速识别常见的激活函数，我们涵盖了传统的激活函数，如Sigmoid、Tanh和ReLU，以及较新的激活函数，如Swish（及相关激活函数）以及Leaky和Parametric ReLU（及相关函数）。

Sigmoid

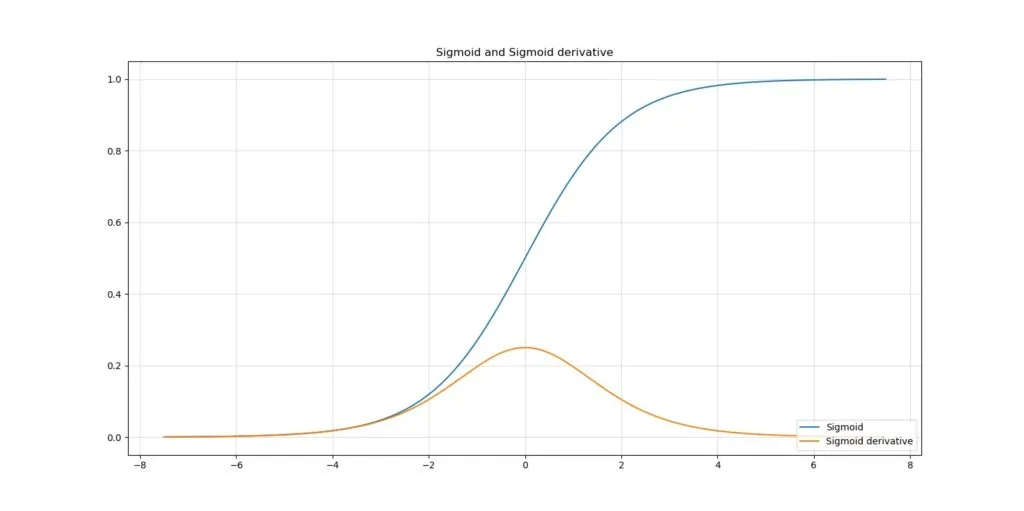
传统的激活函数之一是Sigmoid激活函数。它可能是当今最广为人知且使用最广泛的激活函数之一，仅次于ReLU。它将x ∈ [-∞, +∞]的域转换为y ∈ [0, 1]的范围，其中最大的变化出现在x ∈ [-4, +4]的区间内。

然而，使用Sigmoid可能会为你的机器学习项目引入两个大瓶颈。首先，输出不是关于原点对称的；即，当x = 0时，y = 0.5。这可能会减慢收敛到最优解的速度。

其次，Sigmoid的导数在x = 0时的最大输出约为0.25。这意味着在神经网络优化过程中进行梯度链式传递时，上游层的梯度会非常小。非常大的神经网络会遇到这个问题，即梯度消失问题，它可能会减慢学习速度，甚至使学习变得不可能。

因此，对于当今的机器学习项目来说，如果使用Sigmoid，请记住其局限性，并知道可能有更好的激活函数可用，这是完全可以的。

Tanh

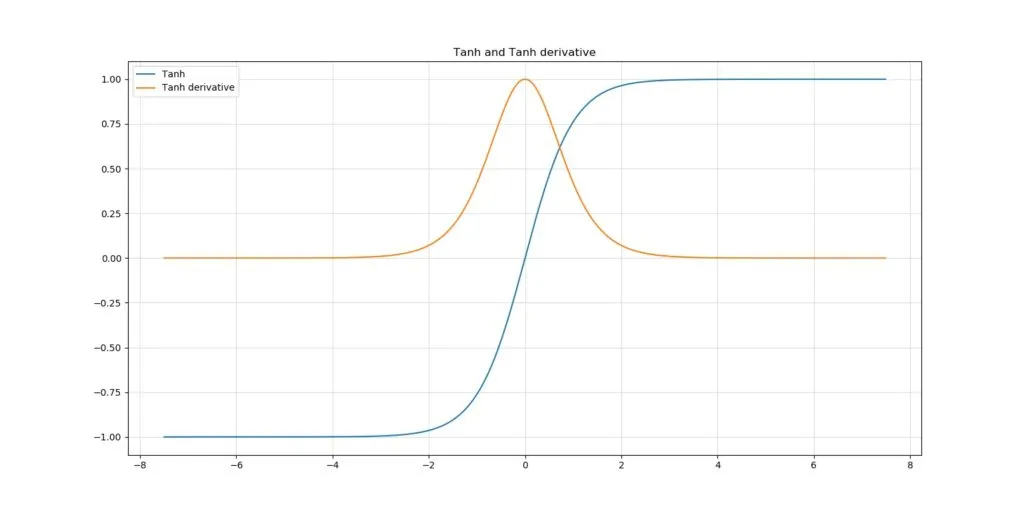
另一种多年来广为人知且常用的激活函数是双曲正切函数，或称为 Tanh 激活函数。它接收整个域内的值，并将其映射到 y ε [-1, +1] 的范围。

尽管它确实提供了关于原点的对称性，但它仍然对梯度消失问题敏感。确定了下一个激活函数来解决这个问题。

修正线性单元（ReLU）

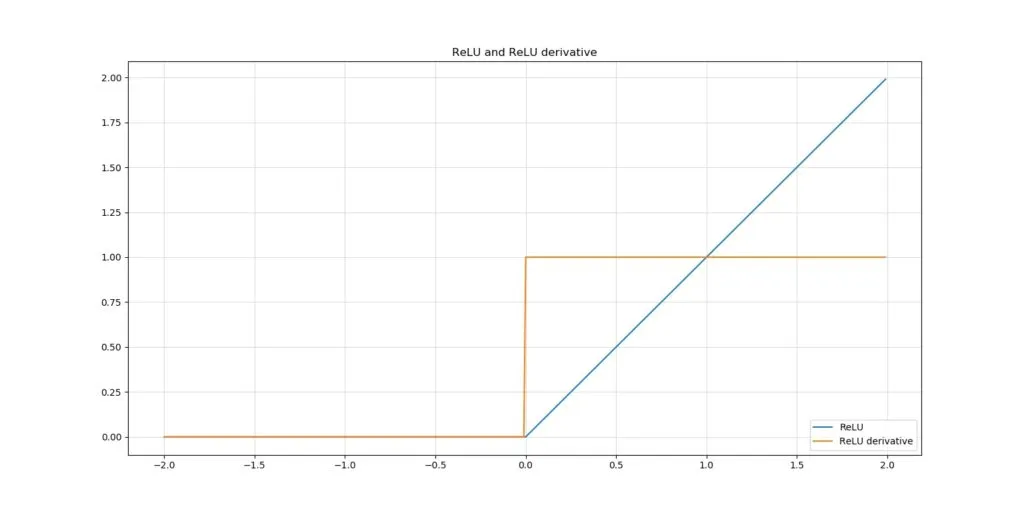
修正线性单元，或称为 ReLU 激活函数，可能是当今最广为人知且最常用的激活函数。对于所有 x > 0 的情况，它输出 x；对于域中的所有其他值，它输出零。

在导数方面，这意味着梯度要么是零，要么是一。这既有好处也有坏处。好处在于模型是稀疏的（所有输入 x < 0 都不被考虑），并且不再出现梯度消失问题（对于正梯度，梯度总是一）。

坏处在于，我们现在让自己面临一个全新的问题：ReLU 死亡问题。有时，所有负输入为零激活所导致的稀疏性效应可能导致太多神经元输出零且无法恢复。换句话说，它们“死亡”了。这也会产生无法再成功学习的模型。

尽管如此，在如今的许多情况下，ReLU 仍然是首选。

带泄漏的修正线性单元（Leaky ReLU）

然而，ReLU 并非解决所有机器学习问题的万能钥匙。在使用它时，你可能会遇到一些问题。

首先，ReLU 不是连续可微的。在 x = 0 这个 x 和 0 的分界点，梯度无法计算。这个问题并不太严重，但可能会略微影响训练性能。

其次，也是更严重的是，ReLU 将所有小于 0 的值设为 0。这在稀疏性方面是有益的，因为网络会适应以确保最重要的神经元的值大于 0。然而，这也是一个问题，因为 0 的梯度是 0，因此到达较大负值的神经元无法从被卡在 0 的状态中恢复。神经元实际上“死亡”了，因此这个问题被称为 ReLU 死亡问题。当你的神经元没有正确初始化或数据没有很好地归一化时，你尤其容易受到这个问题的影响，这会在优化模型的初始阶段导致权重的大幅波动。这个问题的影响可能是你的网络基本上停止学习并且表现不佳。

如果你在 ReLU 的左侧部分（即输出总是 0 的部分）引入一个轻微但显著的信息泄漏，会怎么样呢？

这是带泄漏的修正线性单元（Leaky ReLU）的前提，它是许多较新的激活函数之一，旨在降低对 ReLU 死亡问题的敏感性。

数学上，它的定义如下：

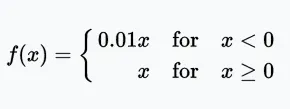
Leaky ReLU 可以可视化如下：

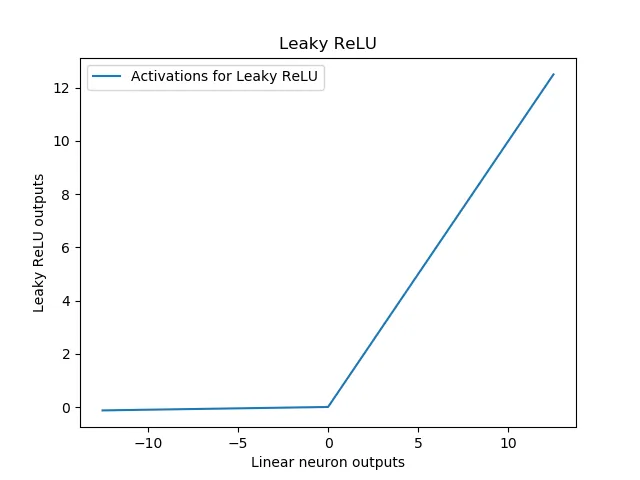
如果你将这与上面传统 ReLU 的图像进行比较，你会发现对于所有小于 0 的输入，输出是略微下降的。其理论依据是，这些小的数值可以减少 ReLU 激活神经元的“死亡”。这样，你就不用太担心神经网络的初始化和数据的归一化问题了。尽管这些话题仍然很重要，但它们的重要性稍微降低了一些。

Leaky ReLU 真的有效吗？

接下来，问题是：Leaky ReLU 真的有效吗？也就是说，它真的能降低 ReLU 激活网络“死亡”的可能性吗？

在 2018 年的一项研究中，Pedamonti 认为 Leaky ReLU 和 ReLU 在 MNIST 数据集上的表现相似。尽管神经网络“死亡”的问题现在在理论上可能已经得到解决，但实际情况可能是这种情况并不经常发生——而在那些情况下，普通的 ReLU 同样有效。“它简单、快速、标准”——有人这样认为。我也倾向于同意这个观点。

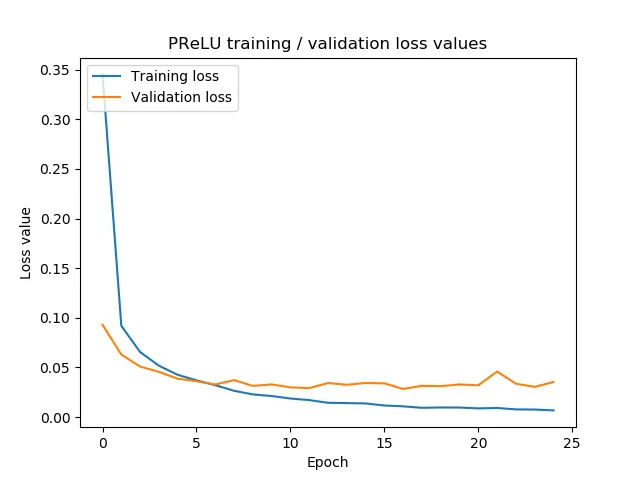
参数化修正线性单元（PReLU）

Leaky ReLU 使用一个必须由机器学习工程师配置的 α 值。从这一点出发进行泛化，参数化修正线性单元（或 PReLU）将这项工作从工程师手中接过，并放入训练过程中。

也就是说，它在神经网络中添加了一些额外的参数，这些参数代表 α 参数（可以是数据每个维度一个 α，也可以是所有维度共用一个 α——这可以由你来设置）。然后，优化过程会确定适合你的数据集的最佳 α，并根据训练进展持续调整它。

ELU

指数线性单元（ELU）激活函数的创建者认识到，Leaky ReLU 和 PReLU 在相当大程度上有助于解决激活函数的问题。然而，他们认为，这些修复方法引入了一个新问题：即不存在“噪声失活状态”，因此，模型对噪声不够鲁棒。

这是什么意思呢？简单地说，负域产生负输出的事实意味着，对于非常大的负数，输出可能仍然相当可观。这意味着噪声仍然可能给模型带来不平衡。

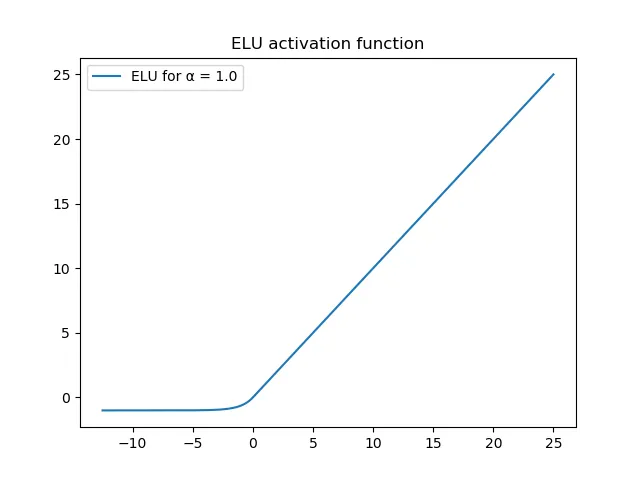
出于这个原因，作者提出了 ELU：一种看起来像 ReLU 的激活函数，在负域有非零输出，然而（连同其梯度）会饱和到某个值（这个值可以通过 α 参数进行配置），从而使模型免受噪声的影响。

ELU 的数学表达式如下：

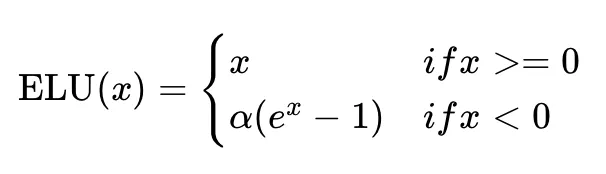
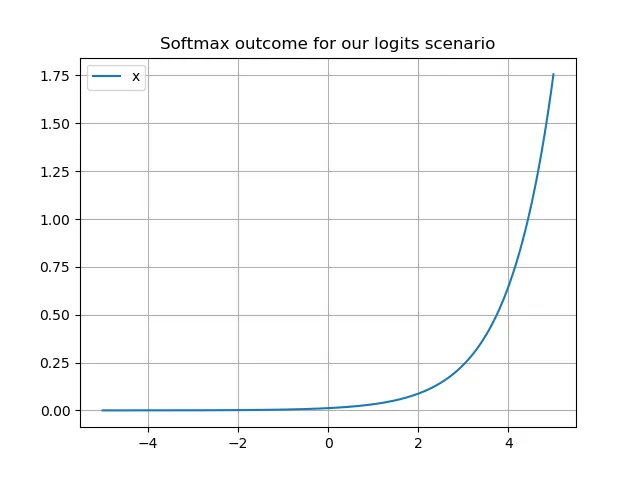
Softmax

现在来点完全不一样的：从用于隐藏层的激活函数，我们将转向一个输出激活函数，作为一个小插曲。让我们来看看 Softmax 激活函数。

Softmax 在分类任务中应用相当广泛，尤其是在你试图用分类交叉熵损失解决多类分类问题时。Softmax 的工作原理非常巧妙且直观：通过将某个向量中的所有值相互关联，并将它们转换为遵循概率论原则的数字，Softmax 基本上是在你的向量值上计算一个离散概率分布。当这些值表示基于神经网络的分类器的输出时，你实际上是在为每个样本计算目标类别上的概率分布。这使你能够选择“最可能的类别”，并且这一特性对基于神经网络的目标检测器等有所贡献。

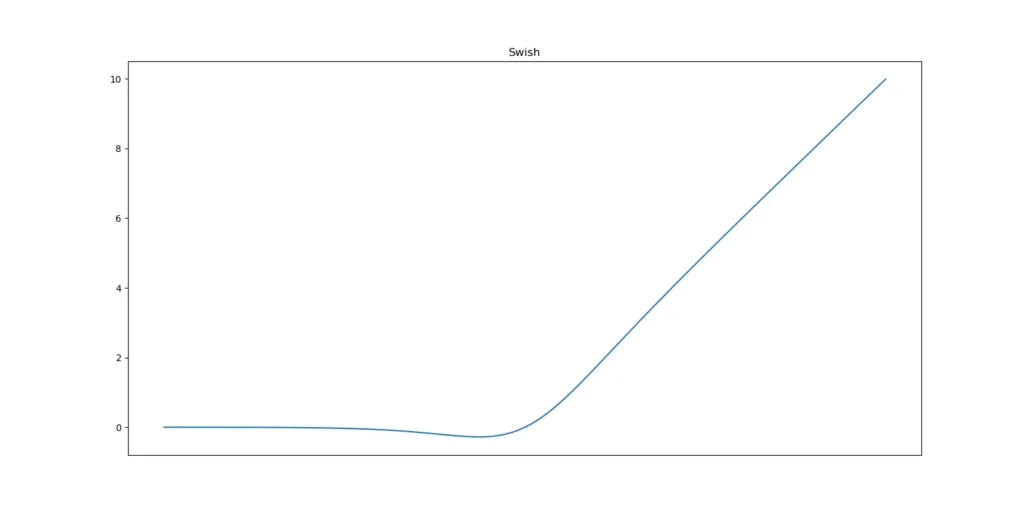
Swish

然而，这并不意味着它不能改进。2017 年 10 月，来自 Google Brain 的 Prajit Ramachandran、Barret Zoph 和 Quoc V. Le 提出了 Swish 激活函数。这是一个相对简单的函数：它是输入 x 与 x 的 sigmoid 函数相乘——其表达式如下。

公式如下：

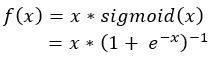
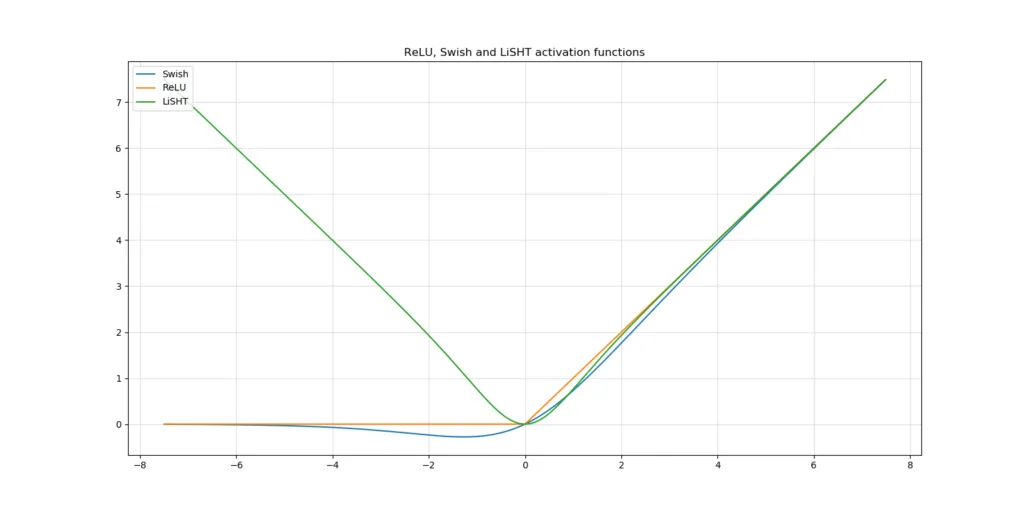
观察这个图像，你可能的第一反应是它看起来很像 ReLU。这个猜测并不差。相反，它确实看起来像这个事实上的标准激活函数，但有一个不同之处：0 附近的区域与 ReLU 不同。

Swish 是一个平滑的函数。这意味着它不会像 ReLU 在 x = 0 附近那样突然改变方向。相反，它从 0 平滑地弯曲到小于 0 的值，然后再向上弯曲。

这个观察意味着它也是非单调的。因此，它不像 ReLU 和其他两个激活函数那样保持稳定或朝一个方向移动。

为什么 Swish 可能比 ReLU 更好

在他们的工作中，Ramachandran 等人写道，他们的“大量实验表明，Swish 在应用于各种具有挑战性的领域（如图像分类和机器翻译）的深度网络上，始终与 ReLU 相当或优于 ReLU”。

这很有趣。之前提出的 ReLU 替代品在各种机器学习任务中表现出了不一致的结果。如果 Swish 如作者所声称的那样，始终与 ReLU 相当或优于 ReLU，那么这将使它成为在全球范围内挑战 ReLU 的候选者！

现在剩下的问题是——如果 Swish 通常比 ReLU 产生更好的结果，为什么会这样？作者提出了各种观察来尝试解释这种行为：

• 首先，它在下方是有界的。因此，Swish 与 ReLU 一样受益于稀疏性。非常负的权重只是被归零。
• 其次，它在上方是无界的。这意味着对于非常大的值，输出不会饱和到最大值（即，对所有神经元为 1）。根据 Swish 论文的作者，这是 ReLU 与更传统的激活函数不同的地方。
• 第三，将 Swish 与 ReLU 区分开来的是，它是一个平滑的曲线，这意味着其输出景观也将是平滑的。这在优化模型以收敛到最小损失方面提供了好处。
• 第四，在 ReLU 中，小的负值被归零（因为对于 x < 0，f(x) = 0）。然而，这些负值可能仍然对于捕获数据底层模式很重要，而大的负值可能被归零（出于稀疏性的原因，如我们上面所见）。平滑性和 x ≈ 0 时 f(x) < 0 的值带来了这一好处。这显然是优于 ReLU 的。

总而言之，如果你在机器学习项目中感到有点想冒险，Swish 激活函数可能是一个值得测试的候选者。也许，在这个过程中你甚至会改进你的模型。

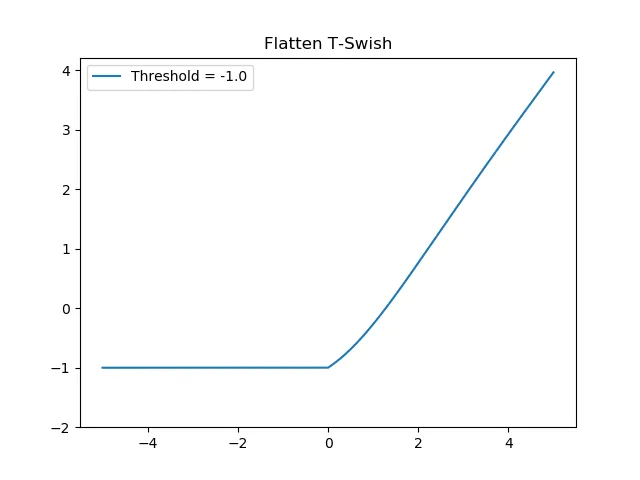
FTSwish

另一种 Swish 风格的激活函数称为 Flatten-T Swish。它有效地将 ReLU 和 Sigmoid 激活函数结合为一个，试图解决与传统激活函数相关的许多问题：

LiSHT

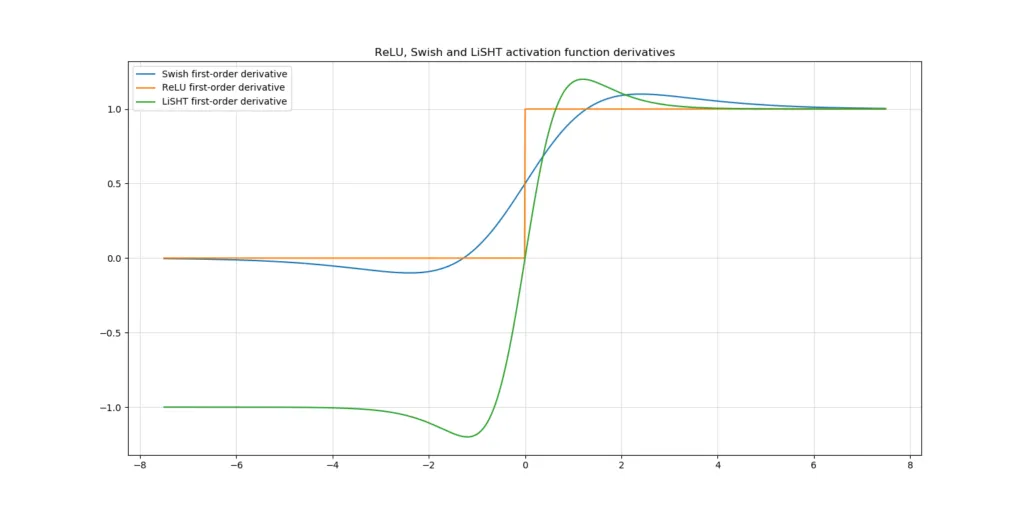
另一种激活函数是 LiSHT。与更传统的激活函数相比，它的工作方式有所不同：负输入被转换为正输出。然而，在导数方面，这会对负输入产生负梯度，这些梯度最终会饱和至零。这可能对模型的稀疏性和训练能力都有好处。因此，它可能值得一试！

LiSHT 在数学上表达和理解起来非常简单：

当我们将其与传统的ReLU和Swish进行比较时，得到了这张图：

当我们从导数的角度来看LiSHT时，我们看到的是这样的：

总结

在这篇文章中，你看到了常用激活函数以及一些较新激活函数的概述，这些新函数旨在解决与这些激活函数相关的问题。最值得注意的是，这些问题包括梯度消失问题和ReLU死亡问题。