在处理表格数据的预测问题时，我们通常会将特征选择作为过程的一部分。这样做至少有几个重要原因，而且每个原因都各不相同。首先，它可以提高模型的准确性；其次，可以降低模型训练和执行的计算成本；第三，它可以使模型更加稳健，并在未来数据上表现良好。

本文是关于特征选择，我将深入探讨前两个目标：最大化准确性和最小化计算。

此外，本文介绍了一种称为基于历史的特征选择（HBFS）的方法。HBFS基于对不同特征子集的实验，学习哪些特征表现良好（以及哪些特征在组合在一起时表现良好）的模式，并据此估计和发现可能表现更好的其他特征子集。

本文提供了一些背景信息，比较了HBFS与其他特征选择方法。

特征选择以提高模型准确性

首先看模型的准确性，我们经常会发现，通过使用比可用特征全集更少的特征，可以获得更高的准确性（无论是通过交叉验证还是在单独的验证集上进行测试）。这可能有点反直觉，因为原则上，包括基于树的模型在内的许多模型（这些模型并不总是，但往往是表格数据预测中表现最好的）理应能够忽略不相关的特征，只使用真正具有预测性的特征。然而在实践中，不相关（或仅具有边缘预测性）的特征往往会使模型产生混淆。

以基于树的模型为例，随着我们在树中向下深入，分裂点的确定是基于越来越少的记录，因此选择不相关特征的可能性越来越大。从模型中移除这些特征，虽然通常不会带来非常大的收益，但往往会显著提高准确性（这里的准确性是一个广义的概念，与用于评估模型的任何指标相关，而不一定是准确性指标本身）。

特征选择以降低计算成本

这里讨论的特征选择的第二个动机是最小化模型的计算成本，这也往往非常重要。减少特征数量可以减少调优、训练、评估、推理和监控所需的时间和处理。

特征选择实际上是调优过程的一部分，但在这里我们考虑的是其他调优步骤，包括模型选择、选择执行的预处理和超参数调优——这些步骤往往非常耗时，但如果事先进行了充分的特征选择，耗时就会减少。

在调优模型时（例如，调优超参数），通常需要训练和评估大量模型，这可能会非常耗时。但是，如果特征数量减少到足够程度，这可以大大加快。

如果使用大量特征，这些步骤可能会慢得多。事实上，使用额外特征的成本可能高到足以抵消使用更多特征带来的性能提升（在存在这种提升的情况下——如前所述，使用更多特征并不一定会提高准确性，实际上可能会降低准确性），因此为了使用更少的特征而接受性能上的小幅下降可能是合理的。

此外，可能还需要减少推理时间。例如，在实时环境中，可能需要非常快速地做出大量预测，而在某些情况下，使用更简单的模型（包括使用更少的特征）可以促进这一点。

在评估方面也有类似的成本，同样在监控每个模型时也是如此（例如，在进行数据漂移测试时，如果监控的特征较少，这会更简单）。

任何准确性提高的业务收益都需要与更复杂模型的成本相权衡。通常情况下，即使准确性只有很小的提升，也可能值得添加额外特征。但相反的情况也经常发生，性能上的小幅提升并不总是能证明使用更大、更慢的模型是合理的。事实上，很多时候，准确性上的小幅提升并没有真正的业务收益。

其他动机

特征选择还可能出于其他动机。在某些环境中，使用比必要特征更多的特征需要在收集、存储以及确保这些特征质量方面付出额外努力。

另一个动机，至少在托管环境中工作时，是使用较少的特征可能会降低总体成本。这不仅仅是因为使用更多特征时增加的计算成本，还可能包括其他成本。例如，在使用Google BigQuery时，查询成本与访问的列数相关，因此使用较少的特征可能会节省成本。

特征选择技术

进行特征选择的方法有很多，对这些方法的分类方式也有很多。我在这里呈现的不是特征选择方法的标准分类形式，但我认为这是一种相当直接且有用的看待问题的方式。我们可以将技术分为两组：

• 单独评估每个特征的预测能力的方法。这些方法包括通常所说的过滤方法，以及一些更复杂的方法。一般来说，这类方法会以某种方式单独评估每个特征，例如，根据它们与目标列的相关性，或它们与目标列的互信息等。这些方法不考虑特征之间的交互作用，可能会遗漏那些仅在与其他特征结合使用时才具有预测性的特征，也可能会包含那些具有预测性但高度冗余的特征，即在其他特征存在的情况下，添加一个或多个特征几乎不会增加额外的预测能力。
• 试图确定一组理想特征的方法。这包括通常所称的包装方法（我将在下面进一步描述）。这还包括遗传方法和其他优化方法（如群体智能等）。这些方法并不试图对每个单独特征的预测能力进行排名，而是寻找一组特征，这些特征组合在一起的效果比任何其他组合都要好。这些方法通常会评估多个候选特征集，然后选择其中最好的一个。这些方法之间的主要区别在于它们如何确定要评估哪些特征集。

单独估计每个特征的预测能力

scikit-learn（以及其他几个库，例如mlxtend）提供了许多特征选择方法。

scikit-learn中的大多数特征选择工具旨在通过评估特征与目标列的相关性来识别最具预测性的特征，且每次只考虑一个特征。这些方法包括，例如，卡方检验、互信息和方差分析F值。

FeatureEngine库还提供了一种称为MRMR的算法实现，该算法同样旨在根据特征与目标的相关性以及与其他特征的关联性来对特征进行排名（它将那些与目标高度相关且与其他特征关联性低的特征排名最高）。

接下来，我们将看看其他一些试图单独评估每个特征的方法。这远非一个完整的列表，但涵盖了许多最受欢迎的方法。

递归特征消除

递归特征消除（Recursive Feature Elimination, RFE）是scikit-learn提供的一种方法，它首先使用全部特征训练一个模型。这个模型必须能够提供特征重要性（例如，随机森林提供feature_importance_属性，或者线性回归可以使用系数来估计每个特征的重要性，前提是特征已经进行了缩放）。

然后，它会反复移除最不重要的特征，并重新评估剩余特征，直到达到目标特征数量。如果这个过程一直进行到只剩下一个特征，那么我们就得到了每个特征预测价值的排名顺序（特征被移除得越晚，其预测性被认为越强）。

一维模型

一维模型是指使用一维，即一个特征的模型。例如，我们可以创建一个决策树，仅使用单个特征来预测目标。可以对数据集中的每个特征逐一训练这样的决策树，并评估每个特征预测目标的能力。对于任何单独具有预测性的特征，相关的决策树将具有优于随机的性能。

使用这种方法，还可以根据使用每个特征训练的一维模型的准确性来对特征进行排名。

这与简单地检查特征与目标之间的相关性有些相似，但也能够检测特征与目标之间更复杂、非单调的关系。

基于模型的特征选择

scikit-learn支持基于模型的特征选择。为此，使用所有特征训练一个模型，就像递归特征消除一样，但我们不是一次移除一个特征，而是直接使用模型提供的特征重要性（或者使用另一个特征重要性工具，如SHAP，来做类似的事情）。例如，我们可以训练一个逻辑回归或随机森林模型。这样做，我们可以访问分配给每个特征的特征重要性，并选择最相关的特征。

如果我们的目标是创建最准确的模型，那么这种方法并不一定是识别最佳特征子集的有效手段，因为它识别的是模型在任何情况下都在使用的特征，而不是模型应该使用的特征。因此，使用这种方法通常不会导致更准确的模型。然而，这种方法非常快，当目标不是提高准确性，而是减少计算量时，这非常有用。

置换测试

置换测试与之类似。这种方法有多种变体，但来看其中一种方法：我们使用全部特征训练一个模型，然后使用验证集或通过交叉验证来评估它。这提供了模型性能的基线。然后，我们可以逐一取出验证集中的每个特征，对其进行打乱（置换），重新评估模型，并确定分数下降了多少。也可以对每个置换后的特征重新训练，一次一个。准确性下降得越多，该特征就越重要。

Boruta方法

在Boruta方法中，我们取每个特征，并创建一个所谓的影子特征，它是原始特征的置换版本。因此，如果我们原本在表中有10个特征，我们为每个特征创建影子版本，因此总共有20个特征。然后，我们使用这20个特征训练一个模型，并评估每个特征的重要性。同样，我们可以使用许多scikit-learn模型和其他模型（如CatBoost）提供的内置特征重要性度量，或者使用SHAP等库（这可能更慢，但会提供更准确的特征重要性）。

我们将给予任何影子特征（假设它们没有预测能力）的最大重要性作为区分预测性和非预测性特征的阈值。检查所有其他特征的特征重要性是否高于这个阈值。这个过程重复多次，并根据每个特征获得高于此阈值的特征重要性的次数对其进行评分。

这是对可能用于单独评估特征的一些方法的快速概述。这些方法可能不是最优的，特别是当目标是创建最准确的模型时，因为它们不考虑特征之间的交互作用，但它们非常快，并且往往能够很好地对特征进行排名。

一般来说，使用这些方法，我们会得到每个特征的排名顺序。我们可能已经提前确定了希望使用的特征数量。例如，如果我们知道希望使用10个特征，我们可以简单地选择排名前10的特征。

或者，我们可以使用验证集进行测试，首先使用排名最靠前的1个特征，然后是前2个，再然后是前3个，依此类推，直到使用所有特征。例如，如果我们有一个特征（从最强到最弱）的排名顺序：{E, B, H, D, G, A, F, C}，那么我们可以测试：{E}，然后是{E, B}，然后是{E, B, H}，依此类推，直到全集{E, B, H, D, G, A, F, C}，其想法是，如果我们只使用一个特征，那么它就是最强的那个；如果我们只使用两个特征，那么它们就是最强的两个，依此类推。根据这些特征集的分数，我们可以选择具有最高指标分数的特征数量，或者选择最能平衡分数和特征数量的特征数量。

寻找最优特征子集

上述方法的主要局限性在于它们没有充分考虑特征之间的交互作用。特别是，它们可能会错过那些单独看并不强大，但在特定数据子集中或与其他特征的某种关系中对目标具有预测作用的特征；同时，它们也可能包含冗余特征。如果两个或多个特征提供了大部分相同的信号，那么很可能其中一些特征可以在几乎不降低模型性能的情况下被移除。

我们现在来看那些试图找到最优特征子集的方法。这些方法并不试图单独评估或排名每个特征，而是致力于找到作为整体表现最佳的特征集。

为了确定最优特征集，有必要测试和评估许多这样的集合，这成本更高——因为组合的数量比单独考虑每个特征时要多，而且由于特征更多，每个组合的评估成本也更高（模型训练速度往往更慢）。不过，这通常能产生比简单使用所有特征或依赖单独评估特征的方法更强的模型。

我应该指出，并不一定非此即彼；完全有可能将这些方法结合起来使用。例如，由于大多数识别最优特征集的方法都相当慢，因此可以先运行上述方法（即单独评估特征然后排名其预测能力）来创建一个特征短名单，然后执行一种方法来找到这些短名单特征的最优子集。这种方法可能会错误地排除一些特征（首先用于过滤特征的方法可能会移除一些在其他特征存在时会有用的特征），但也可以在较快但不太准确的方法和较慢但更准确的方法之间取得良好的平衡。

试图找到最佳特征集的方法包括所谓的包装器方法、随机搜索和各种优化方法，以及一些其他方法。本文介绍的HBFS方法也是寻求找到最优特征集的方法之一。下面将对这些方法进行描述。

包装器方法

包装器方法也可以被视为一种对特征进行排名的技术（它们可以提供估计预测能力的排名顺序），但在此讨论中，我将它们归类为寻找其能够识别的最佳特征集的方法。包装器方法确实会测试特征的全组合，但以一种受限（尽管通常仍然非常慢）的方式进行。

在包装器方法中，我们通常要么从一个空特征集开始，并逐个添加特征（这被称为添加过程），要么从完整的特征集开始，并逐个移除特征（这被称为减去过程）。

在添加过程中，我们首先找到能够创建最强模型的单个特征（使用相关指标）。这需要逐个测试每个特征。然后，我们找到当添加到集合中时，能够使我们使用第一个特征和第二个特征创建的最强模型的第二个特征。这需要测试除已存在特征外的每个特征。然后，我们以同样的方式选择第三个特征，依此类推，直到最后一个特征，或直到达到某个停止条件（如最大特征数）。

如果有特征集{A, B, C, D, E, F, G, H, I, J}，共有10个特征。我们首先逐个测试这10个特征（需要10次测试）。我们可能会发现D效果最好，因此特征集为{D}。然后，我们测试{D, A}、{D, B}、{D, C}、{D, E}、…、{D, J}，这是9次测试，并选择其中最强的。我们可能会发现{D, E}效果最好，因此特征集为{D, E}。然后，我们测试{D, E, A}、{D, E, B}、…、{D, E, J}，这是8次测试，并再次选择其中最强的，依此类推。如果目标是找到最佳的5个特征集，我们最终可能会得到，例如，{D, E, B, A, I}。

我们可以看出，这种方法可能会错过最佳的5个特征组合，但通常会表现得相当不错。在这个例子中，这很可能是可以识别的最强大小为5的子集之一，测试表明包装器方法的效果往往不如预期。

我们还可以看出，如果特征很多，这种方法可能会非常慢。如果有数百个特征，这将是不可能的。但是，在特征数量适中的情况下，这种方法可以相当有效地工作。

减去方法的工作原理类似，但在每一步中移除一个特征。

随机搜索

随机搜索在特征选择中很少使用，尽管它在许多其他场景（如超参数调优）中都有应用。

这可能导致随机搜索不必要地测试那些肯定表现不佳的候选特征集（例如，与已经测试过且表现不佳的特征集非常相似的候选特征集）。它也可能导致未能测试那些根据迄今为止进行的其他实验来看，似乎最有前途的特征组合。

然而，随机搜索非常简单，在许多情况下都足够适用，并且往往优于那些单独评估特征的方法。

优化技术

有许多优化技术可用于识别最佳特征集，包括爬山算法、遗传方法、贝叶斯优化和群体智能等。

应用于特征选择的爬山算法可以与“使用爬山算法解决经典世界职业棒球大赛投注问题”中描述的过程类似。

在这里，我们会从一个随机的特征集开始，然后找到一个小的修改（添加或移除少量特征）来改善这个集合（测试几个这样的小修改，并选择其中最好的），接着再找到一个小的改变来进一步改善这个特征集，如此反复，直到满足某些停止条件（我们可以限制时间、考虑的候选数量、自上次改进以来的时间，或设置其他此类限制）。

通过这种方式，从一个随机（且可能表现不佳）的特征集开始，我们可以逐步且反复地对其进行改进，发现越来越强的特征集，直到最终发现一个非常强的特征集。

例如，我们可能随机从{B, F, G, H, J}开始，然后发现小的变化{B, C, F, G, H, J}（添加了特征C）效果更好，接着发现{B, C, F, H, J}（移除了特征G）效果又稍微好了一些，如此继续。

在某些情况下，我们可能会陷入局部最优，此时另一种称为模拟退火的技术可能有助于继续取得进展。这允许我们偶尔选择表现较差的选项，从而有助于防止陷入一种无法通过小改变来改进的状态。

遗传算法的工作原理类似，但在每一步中，会考虑多个候选者，而不是只有一个，并且除了变异（在爬山解决方案中，对候选特征集进行的每次小修改类似于遗传算法中对候选者进行的修改，在遗传算法中称为变异）外，还会进行组合。

在组合过程中，会选择两个或多个候选者，并基于这些候选者的某种组合创建一个或多个新的候选者。例如，如果我们有两个特征集，可以取其中一个特征集的一半特征，加上另一个特征集的一半特征，去除任何重复的特征，并将其视为一个新的候选者。

（在实际应用中，使用遗传方法解决特征选择问题时，候选者通常会格式化为一个由0和1组成的字符串——每个特征一个值——按照特征的有序列表排列，指示该特征是否包含在集合中，因此结合两个候选者的过程可能与这个示例略有不同，但原理相同。）

贝叶斯优化

在贝叶斯优化中，解决如寻找最优特征集等问题的方法是，首先尝试一定数量的随机候选特征集，对这些候选集进行评估，然后创建一个模型，该模型能够基于到目前为止已评估的候选集来估计其他特征集的性能。

为此，我们使用一种称为高斯过程的回归器，因为它不仅能够为任何其他候选集（在此情况下，即估计使用此特征集训练的模型将获得的度量分数）提供估计，还能够量化不确定性。

例如，如果我们已经评估了某个特征集，比如{F1, F2, F10, F23, F51}（得分0.853），那么对于非常相似的特征集，比如{F1, F2, F10, F23, F51, F53}，我们可以相对确定地预测其得分，比如0.858。尽管我们不能完全确定，因为新增的特征F53可能会提供大量额外信息。但是，我们的估计将比完全不同的特征集（例如{F34, F36, F41, F62}）更为确定（假设尚未评估过与此类似的特征集，因此其不确定性较高）。

再举一个例子，特征集{F1, F2, F10, F23}比前一个少了一个特征F51。如果F51似乎不具有预测性（考虑到其他包含或不包含F53的特征集的得分），或者与F1高度冗余，那么我们可以有一定信心地估计{F1, F2, F10, F23}的得分，它应该与{F1, F2, F10, F23, F51}的得分大致相同。仍然存在显著的不确定性，但再次强调，这种不确定性远低于完全不同的特征集。

因此，对于任何给定的特征集，高斯过程不仅可以生成其得分的估计值，还可以提供不确定性的形式，即可信区间。例如，如果我们关注的是宏F1分数，高斯过程可以学习估计任何给定特征集的宏F1分数。对于某一特征集，它可能估计得分为0.61，并指定可信区间为0.45至0.77，这意味着有90%的概率（如果我们使用90%的宽度来定义可信区间）F1分数会在0.45和0.77之间。

贝叶斯优化旨在平衡探索和利用。在过程的开始阶段，我们更倾向于探索——在此情况下，即找出哪些特征具有预测性，哪些特征最好一起包含等。然后，随着时间的推移，我们更倾向于利用——利用我们所学来尝试识别尚未评估的最有前景的特征集，并对其进行测试。

贝叶斯优化通过交替使用所谓的采集方法来识别下一个要评估的候选集，评估这些候选集，从中学习，再次调用采集方法，如此循环往复。在早期阶段，采集方法倾向于选择看起来有前景但不确定性高的候选集（因为这些是我们能从中学习最多的），而在后期阶段，则选择看起来最有前景且不确定性相对较低的候选集（因为这些最有可能优于已经评估过的候选集，尽管它们往往是迄今为止发现的得分最高的特征集的小幅变体）。

基于历史的特征选择

我们现在已经快速概述了许多当今常用的其他主要特征选择选项。接下来，我将介绍历史基特征选择（HBFS）。这是另一种我发现相当有用的特征选择方法，而且我并未意识到有其他实现或甚至讨论过这种方法，尽管其想法相当直观和简单。

由于我没有意识到有其他实现，因此我创建了一个Python实现，现已在GitHub上可用，名为HistoryBasedFeatureSelection。

该仓库提供了Python代码、文档、示例笔记本以及用于相当彻底地测试HBFS的文件。

即使你实际上并不使用HBFS来构建机器学习模型，我也希望你能发现这种方法很有趣。这些想法仍然很有用，并且至少是一种有助于思考特征选择的良好方式。

不过，我将展示HBFS与其他特征选择选项相比往往表现相当有利，因此它可能值得在项目中进行考虑，尽管这些想法足够简单，可以直接编码实现——使用GitHub页面上的代码可能很方便，但并非必要。

我将这种方法称为历史基特征选择（HBFS），因为它通过尝试特征子集的历史来学习，从它们在验证集上的表现中学习，测试额外的候选特征集，从这些学习中学习，以此类推。随着实验历史的推进，模型能够越来越好地学习哪些特征子集最有可能表现良好。

以下是主要算法，以伪代码形式呈现：

Loop a specfied number of times (by default, 20)
| Generate several random subsets of features, each covering about half 
|     the features
| Train a model using this set of features using the training data
| Evaluate this model using the validation set
| Record this set of features and their evaluated score
Loop a specified number of times (by default, 10)
|   Train a RandomForest regressor to predict, for any give subset of 
|      features, the score of a model using those features. This is trained
|      on the history of model evaluations of so far.
|  
|   Loop for a specified number of times (by default, 1000)
|   |   Generate a random set of features
|   |   Use the RandomForest regressor estimate the score using this set 
|   |     of features
|   |   Store this estimate
|
|   Loop over a specfied number of the top-estimated candidates from the 
|   |       previous loop (by default, 20)
|   |   Train a model using this set of features using the training data
|   |   Evaluate this model using the validation set
|   |   Record this set of features and their evaluated score   
output the full set of feature sets evaluated and their scores, 
   sorted by scores

我们可以看到，这种方法比贝叶斯优化要简单一些，因为第一次迭代完全专注于探索（候选者是随机生成的），而所有后续的迭代则完全专注于利用——并没有逐渐转向更多利用的趋势。

这种方法有一些好处，因为该过程通常只需要少数几次迭代，通常在4到12次左右（因此，探索那些可能表现较弱的候选特征集的价值较低）。同时，它也避免了调整探索和利用之间平衡的过程。

因此，获取函数相当直接——我们只需选择那些尚未测试但看起来最有前途的候选者。虽然这种方法（由于减少了部分探索）可能会错过一些具有强大潜力的候选者，但在实践中，它似乎能够可靠且相当地快速地识别出最强的候选者。

HBFS（假设为某特征选择方法的缩写）执行速度相当快。当然，它比单独评估每个特征的方法要慢，但在性能方面，它与包装方法、遗传方法以及其他寻求找到最强特征集的方法相比，表现相当不错。

HBFS旨在让用户在其执行过程中理解它所进行的特征选择过程。例如，它提供的一种可视化图表绘制了所有被评估特征集的分数（包括估计分数和实际评估分数），这有助于我们理解它对于任意候选特征集所能给出的分数估计得有多准确。

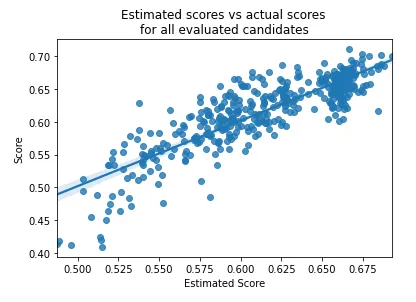
HBFS还包括一些在特征选择方法中不常见的功能，例如允许用户选择：1) 单纯最大化准确性，或2) 在最大化准确性与最小化计算成本之间取得平衡。

结论

本文简要概述了一些最常见的特征选择方法。每种方法的工作原理略有不同，各有优缺点。根据具体情况，以及目标是最大化准确性还是在准确性与计算成本之间取得平衡，不同的方法可能更受青睐。

本文还非常简要地介绍了基于历史的特征选择（HBFS）方法。

HBFS是我发现的一种效果非常好的新算法，通常（但并非总是）优于本文描述的其他方法（没有任何一种方法能在所有情况下都严格优于其他方法）。