时间序列数据往往包含隐藏的周期性模式，这些模式通过直接观察很难识别。傅里叶变换提供了一种数学框架，可以将这些复杂信号分解为它们的基本频率成分，从而揭示出可能不易察觉的潜在模式和周期。

傅里叶变换将时间序列从时域（随时间观察的数据）转换到频域（作为周期信号的数据）。本质上，它将时间序列表示为具有不同频率和振幅的正弦波和余弦波的和。

为什么在时间序列中使用傅里叶变换？

金融市场利用傅里叶分析来检测资产价格中的交易周期和季节性模式。通过将价格变动分解为其频率成分，分析师可以区分短期波动和长期趋势，从而为交易策略和风险管理决策提供依据。

在工程应用中，傅里叶变换有助于识别机械振动模式，从而在设备故障之前进行预测性维护。频域分析能够揭示原始时间序列数据中可能无法察觉的运行条件的微妙变化。

气候科学家利用这些技术来分析温度和降水模式，识别自然周期和潜在异常。分离不同频率成分的能力有助于区分季节性变化和长期气候趋势。

傅里叶变换在检测数据中的周期、季节性或重复结构以及过滤噪声方面非常有用。

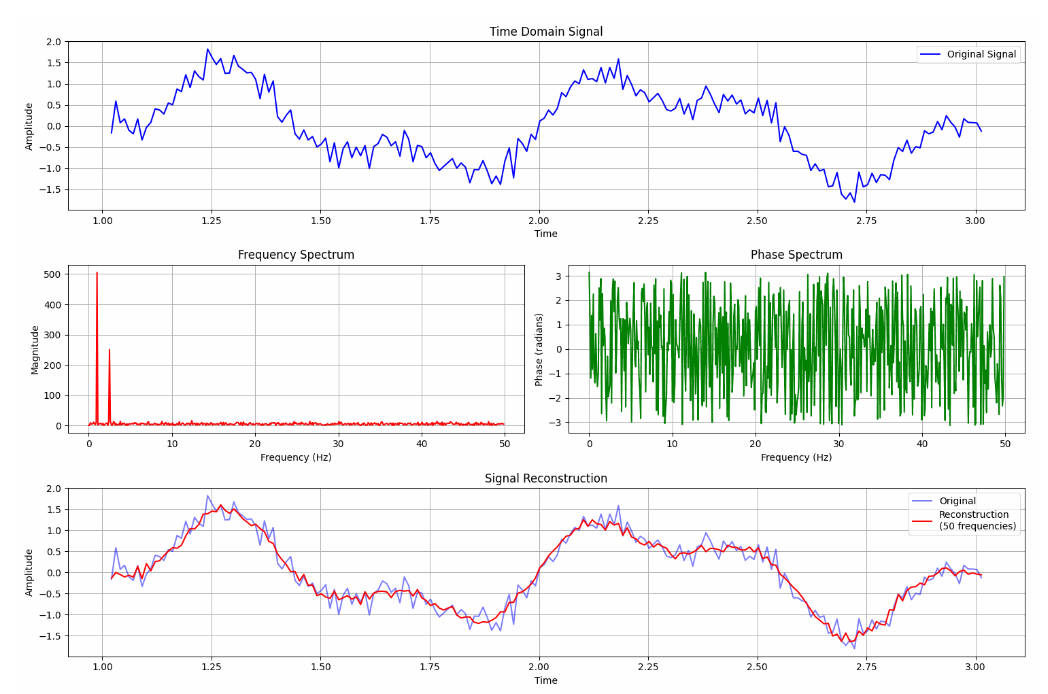
让我们来构建一个例子

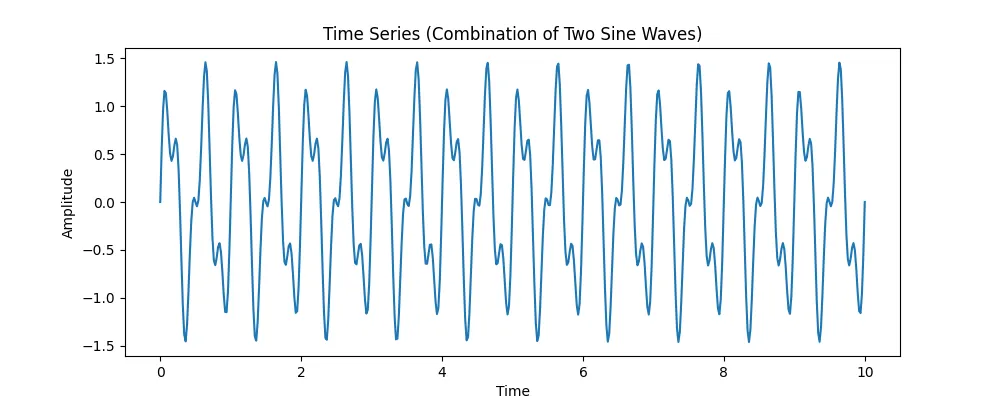
假设我们有一个合成时间序列，它结合了两种不同频率的正弦波。

import numpy as np
import matplotlib.pyplot as plt
# Generate a time series with two frequencies
np.random.seed(42)
time = np.linspace(0, 10, 500)  # 500 time points
freq1, freq2 = 2, 5  # Frequencies in Hz
signal = np.sin(2 * np.pi * freq1 * time) + 0.5 * np.sin(2 * np.pi * freq2 * time)
# Plot the time series
plt.figure(figsize=(10, 4))
plt.plot(time, signal)
plt.title("Time Series (Combination of Two Sine Waves)")
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.show()

傅里叶变换分析频率

应用傅里叶快速变换（FFT）来分析频率并提取频率成分。

# Apply Fourier Transform
fft_result = np.fft.fft(signal)
# Frequency axis
frequencies = np.fft.fftfreq(len(fft_result), d=(time[1] - time[0]))  
# Plot the magnitude spectrum
plt.figure(figsize=(10, 4))
plt.plot(frequencies[:len(frequencies)//2], np.abs(fft_result)[:len(fft_result)//2])
plt.title("Frequency Domain Representation")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
plt.show()

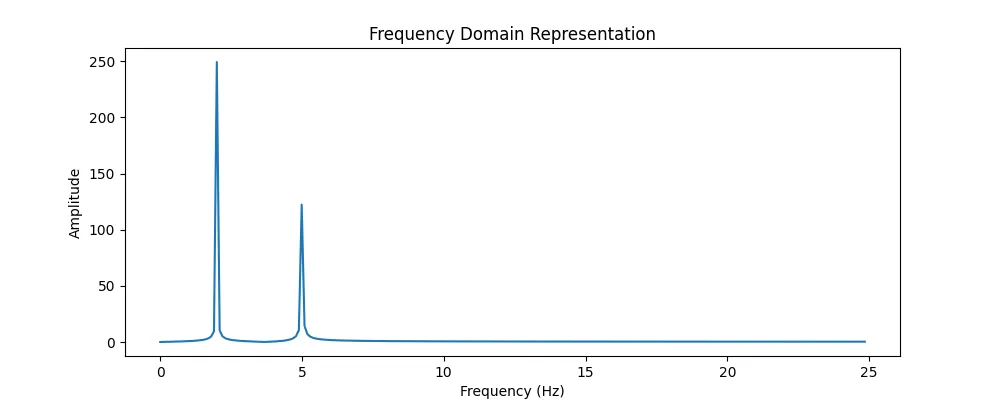
我们看到了什么？

该图在2 Hz和5 Hz处显示出峰值，这与时间序列中的两个频率相对应。这些峰值表明了数据中的主要周期。

示例2：对现实世界数据进行傅里叶变换

让我们使用傅里叶变换来分析一个季节性时间序列，比如航空乘客数据集。

#from sktime.datasets import load_airline
import numpy as np
import matplotlib.pyplot as plt
# Load the Airline Passengers Dataset
y = load_airline()
y = y.values
# Create time array
time = np.arange(len(y))
# Apply Fourier Transform
fft_result = np.fft.fft(y)
frequencies = np.fft.fftfreq(len(fft_result), d=1)  # Assume monthly data (d=1)
# Plot the original time series
plt.figure(figsize=(10, 4))
plt.plot(y)
plt.title("Original Airline Passenger Data")
plt.xlabel("Time")
plt.ylabel("Passengers")
plt.show()
# Plot the frequency domain
plt.figure(figsize=(10, 4))
plt.plot(frequencies[:len(frequencies)//2], np.abs(fft_result)[:len(fft_result)//2])
plt.title("Frequency Domain of Airline Passenger Data")
plt.xlabel("Frequency")
plt.ylabel("Amplitude")
plt.savefig('time_series_passanger.png')
plt.show()

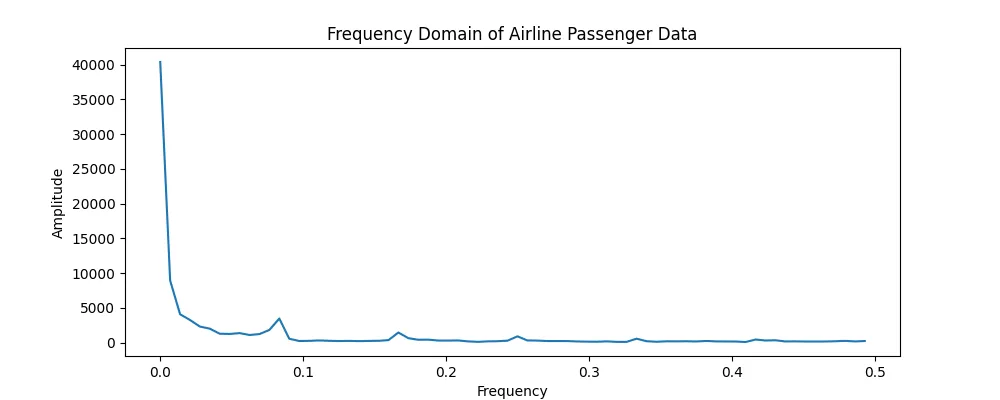
这揭示了什么？

频域图显示了一个明显的峰值，对应于年度季节性周期（频率=1/12个月）。这证实了航空乘客数据中存在的已知季节性。

示例3：利用傅里叶变换过滤噪声

我们可以使用傅里叶变换来过滤掉高频噪声。

# Add random noise to the signal
noisy_signal = y + np.random.normal(0, 50, len(y))
# Apply Fourier Transform to noisy signal
fft_result_noisy = np.fft.fft(noisy_signal)
# Filter out high frequencies
fft_filtered = fft_result_noisy.copy()
threshold = 0.1  # Adjust this threshold as needed
fft_filtered[np.abs(frequencies) > threshold] = 0
# Inverse FFT to get the filtered signal
filtered_signal = np.fft.ifft(fft_filtered)
# Plot the original, noisy, and filtered signals
plt.figure(figsize=(10, 6))
plt.plot(time, noisy_signal, label="Noisy Signal", alpha=0.5)
plt.plot(time, filtered_signal.real, label="Filtered Signal", color='red')
plt.title("Noise Filtering with Fourier Transform")
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.legend()
plt.savefig('time_series_passanger_amp.png')
plt.show()

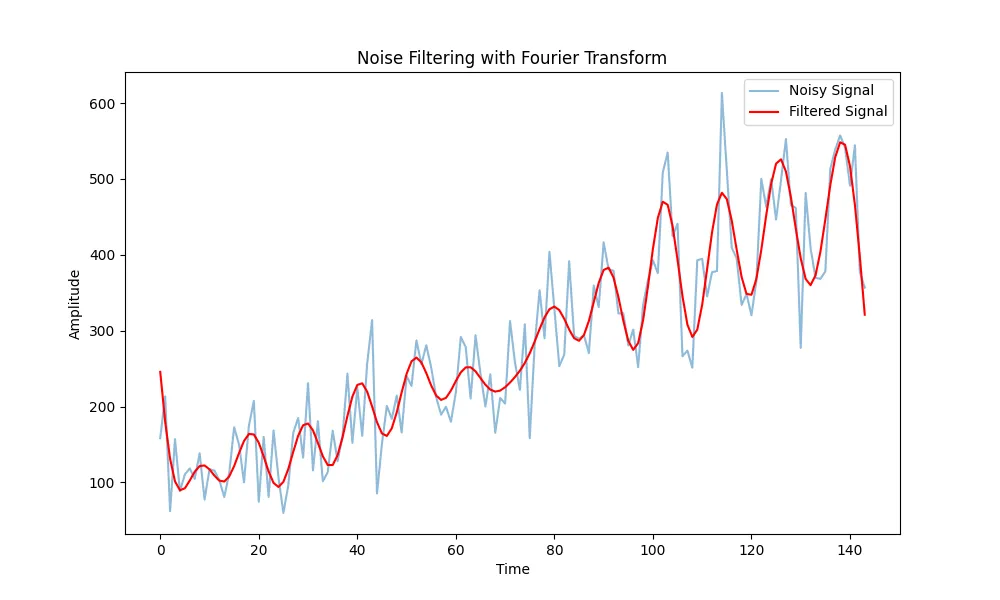
我们看到了什么？

过滤后的信号与原始信号非常吻合，这表明傅里叶变换可以在保留关键模式的同时有效地去除噪声。

对于极大数据集：FFTW

对于非常大的数据集或性能关键型应用，可以使用FFTW（西方最快的傅里叶变换）或其他专用库来进行更快的FFT计算。

Python的scipy.fft模块提供了FFTW的绑定，为某些场景提供了改进的性能。

from scipy.fft import fft, ifft
# Perform FFT with SciPy (uses FFTW internally for optimization)
fft_result = fft(signal)
ifft_result = ifft(fft_result)

高级应用

现代应用通常将傅里叶分析与机器学习技术相结合。通过傅里叶变换提取的频域特征作为神经网络和其他算法的输入，增强了模式识别和预测能力。

信号滤波应用使用傅里叶变换来去除噪声，同时保留数据的基本特征。这种技术在处理传感器数据时特别有价值，因为高频噪声可能会掩盖感兴趣的底层模式。

实施考虑

虽然傅里叶变换提供了强大的分析能力，但正确的实施需要仔细考虑采样率、窗口大小和潜在的混叠效应。快速傅里叶变换（FFT）算法提供了高效的计算，但用户必须了解其假设和限制，以避免对结果的误解。

那么，这意味着什么？

傅里叶变换帮助我们从原始数据中提取有意义的见解。它们揭示隐藏模式的能力，结合现代计算技术的有效实施，使得傅里叶变换在金融分析到科学研究等应用中不可或缺。随着数据复杂性的增加，这些技术在从时间序列数据中提取可操作的信息方面变得越来越有价值。