状态空间模型通过建模生成可观测数据的潜在、未观测状态来分析时间序列。卡尔曼滤波器作为这一方法的基石，为实时估计这些隐藏状态提供了优雅的解决方案。本文探讨了这些方法的理论基础和实际应用，展示了它们在各种应用中的多功能性。

状态空间模型的数学基础

状态空间模型通过一对方程来描述动态系统。状态转移方程，也称为过程模型，数学上捕捉了系统状态如何从一个时间步长到下一个时间步长发生变化，同时包含了确定性动力学和过程噪声。这个方程是预测系统行为的核心，代表了可能无法直接观测到的内部动力学。

观测方程，也称为测量模型，建立了隐藏系统状态与实际可以观测或测量的量之间的数学关系。这个方程至关重要，因为它允许我们从外部测量中推断出内部状态的信息，同时考虑了测量噪声和传感器特性。

这些方程构成了实施各种状态估计技术的基础，从简单的卡尔曼滤波器到更复杂的非线性估计器。这种数学结构为在众多应用中建模和分析动态系统提供了一种强大而灵活的方法。

import numpy as np
class StateSpaceModel:
    def __init__(self, state_dim, observation_dim):
        # State transition matrix (F)
        self.F = np.eye(state_dim)
        # Observation matrix (H)
        self.H = np.zeros((observation_dim, state_dim))
        self.H[0, 0] = 1
        # Process noise covariance (Q)
        self.Q = np.eye(state_dim) * 0.1
        # Observation noise covariance (R)
        self.R = np.eye(observation_dim) * 1.0
        # Initial state mean and covariance
        self.x0 = np.zeros(state_dim)
        self.P0 = np.eye(state_dim)

卡尔曼滤波器算法

卡尔曼滤波器是一种用于受高斯噪声分布影响的线性系统的递归估计算法。该滤波器通过数学上严谨的方式将模型预测与传感器测量相结合，实现最优状态估计。该算法通过两步过程运作，随着新数据的获得，不断细化其估计值。

预测步骤，也称为时间更新，使用系统模型预测下一个状态及其相关的不确定性协方差。此步骤根据已知的系统动力学，将当前状态估计在时间上前向投影，同时考虑任何控制输入和过程噪声。预测方程同时传播状态估计及其不确定性，为下一个时间步提供先验估计。

更新步骤，或测量更新，结合新的传感器测量值来细化预测的状态估计。当获得新的观测值时，滤波器计算卡尔曼增益——一个平衡预测和测量之间相对不确定性的加权因子。该增益用于最优地结合预测和新测量值，从而得到改进的后验状态估计和更新的不确定性协方差。这两个步骤的递归性质使得卡尔曼滤波器在计算上高效，并且适用于实时应用。

class KalmanFilterCustom:
    def __init__(self, state_space_model):
        self.model = state_space_model
        self.state_dim = len(state_space_model.x0)
        self.x = self.model.x0
        self.P = self.model.P0
def predict(self):
        """Prediction step"""
        self.x = self.model.F @ self.x
        self.P = self.model.F @ self.P @ self.model.F.T + self.model.Q
        return self.x, self.P
    def update(self, measurement):
        """Update step"""
        y = measurement - self.model.H @ self.x  # Innovation
        S = self.model.H @ self.P @ self.model.H.T + self.model.R  # Innovation covariance
        K = self.P @ self.model.H.T @ np.linalg.inv(S)  # Kalman gain
        self.x = self.x + K @ y  # Update state
        self.P = (np.eye(self.state_dim) - K @ self.model.H) @ self.P  # Update covariance
        return self.x, self.P

实践示例：追踪移动物体

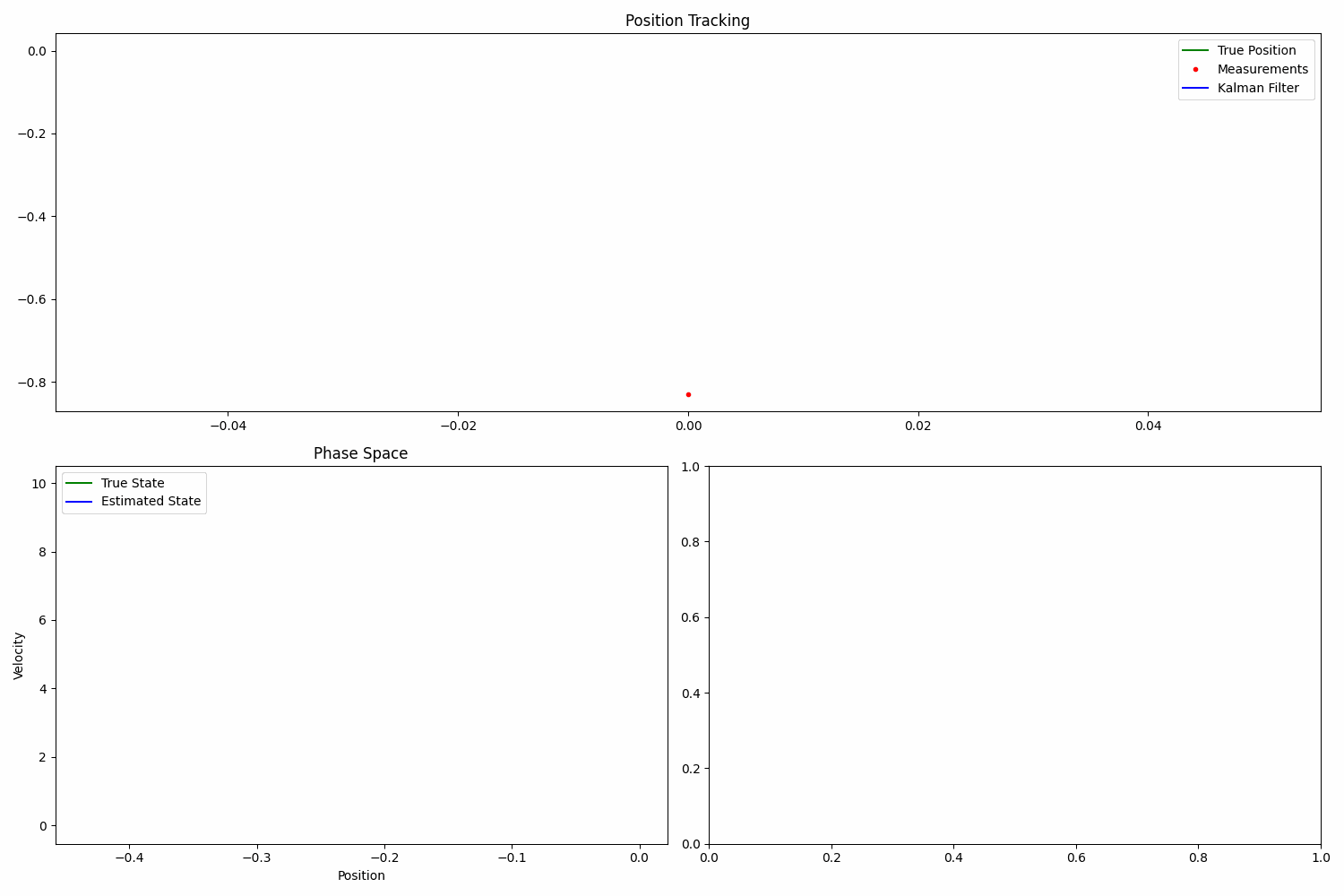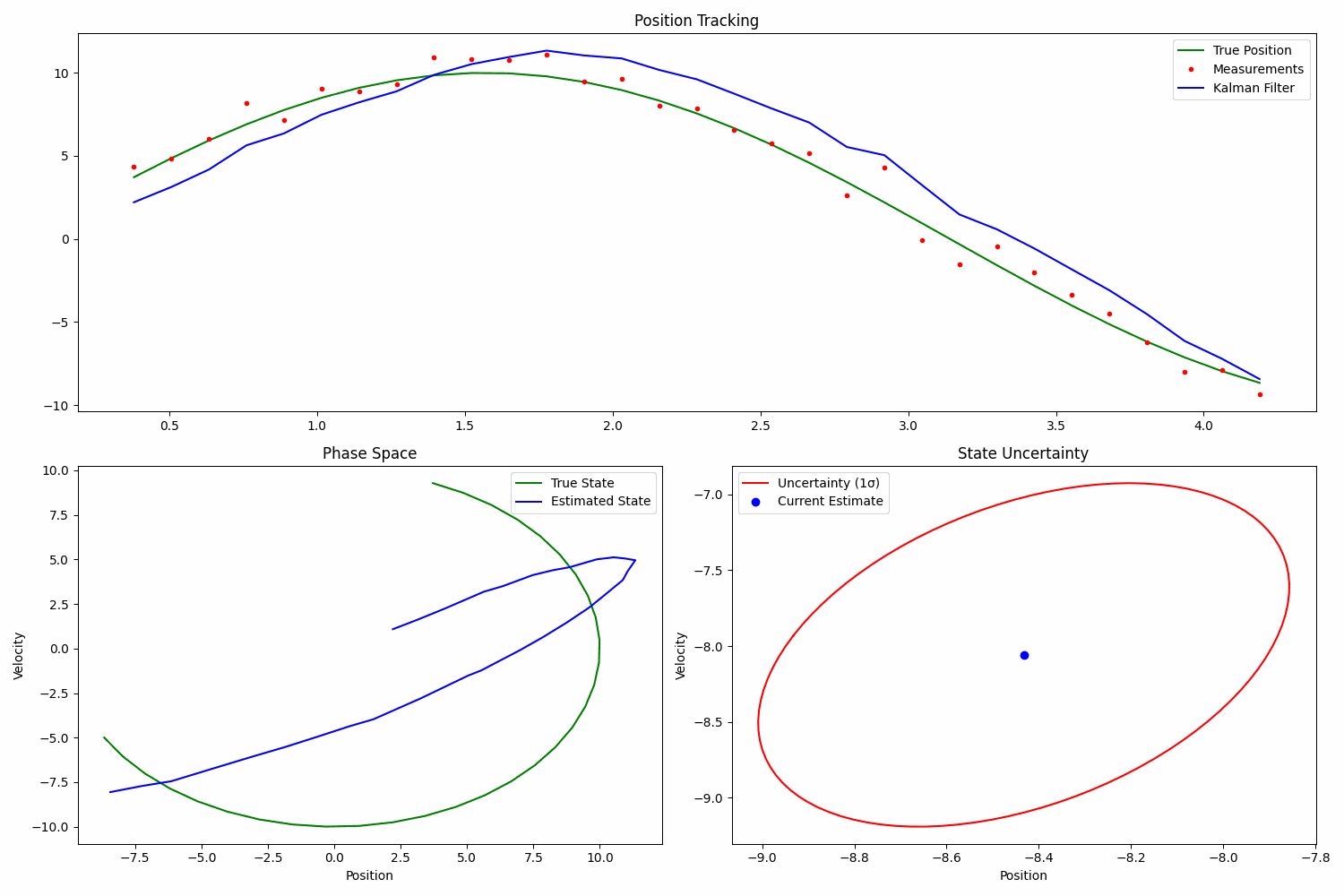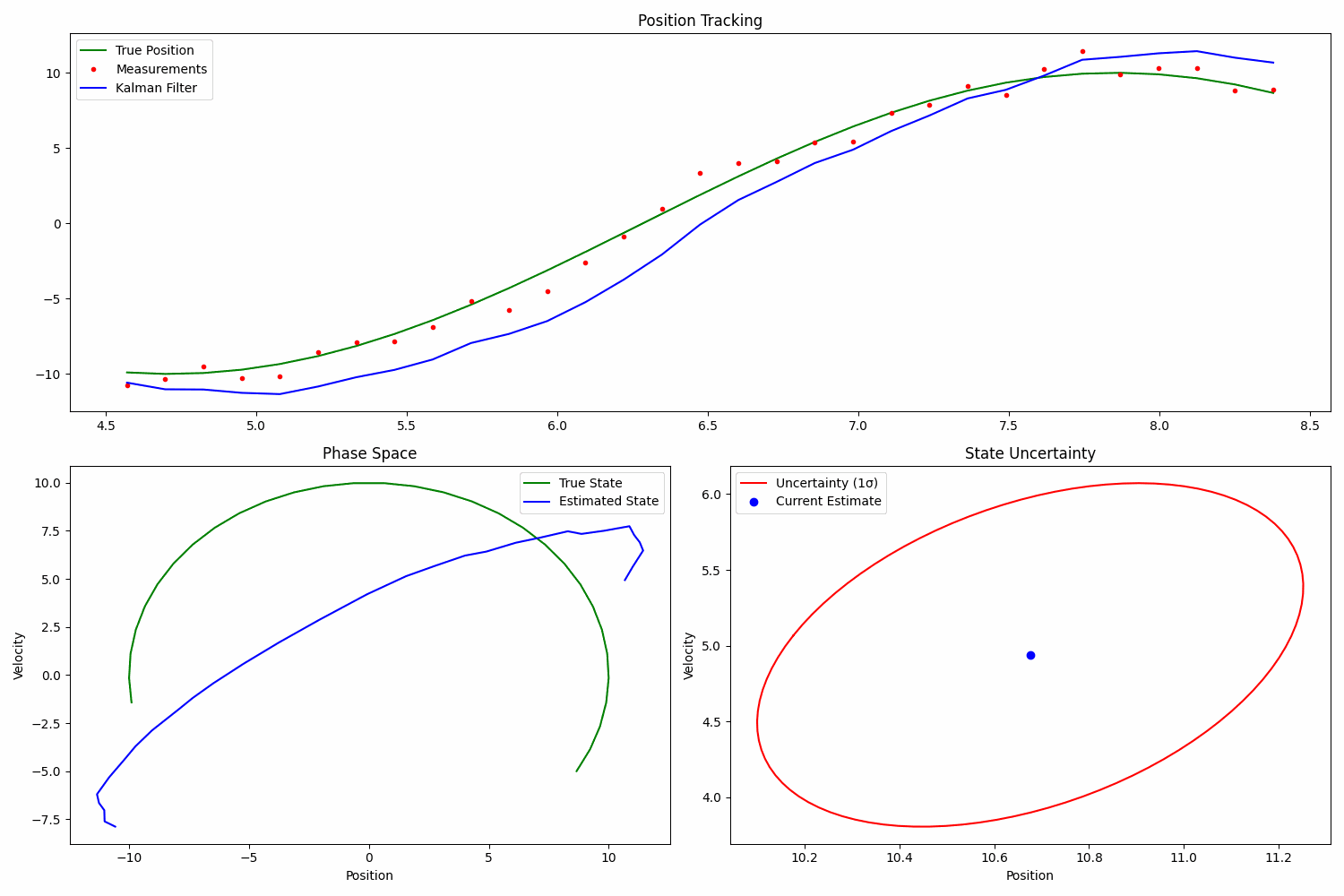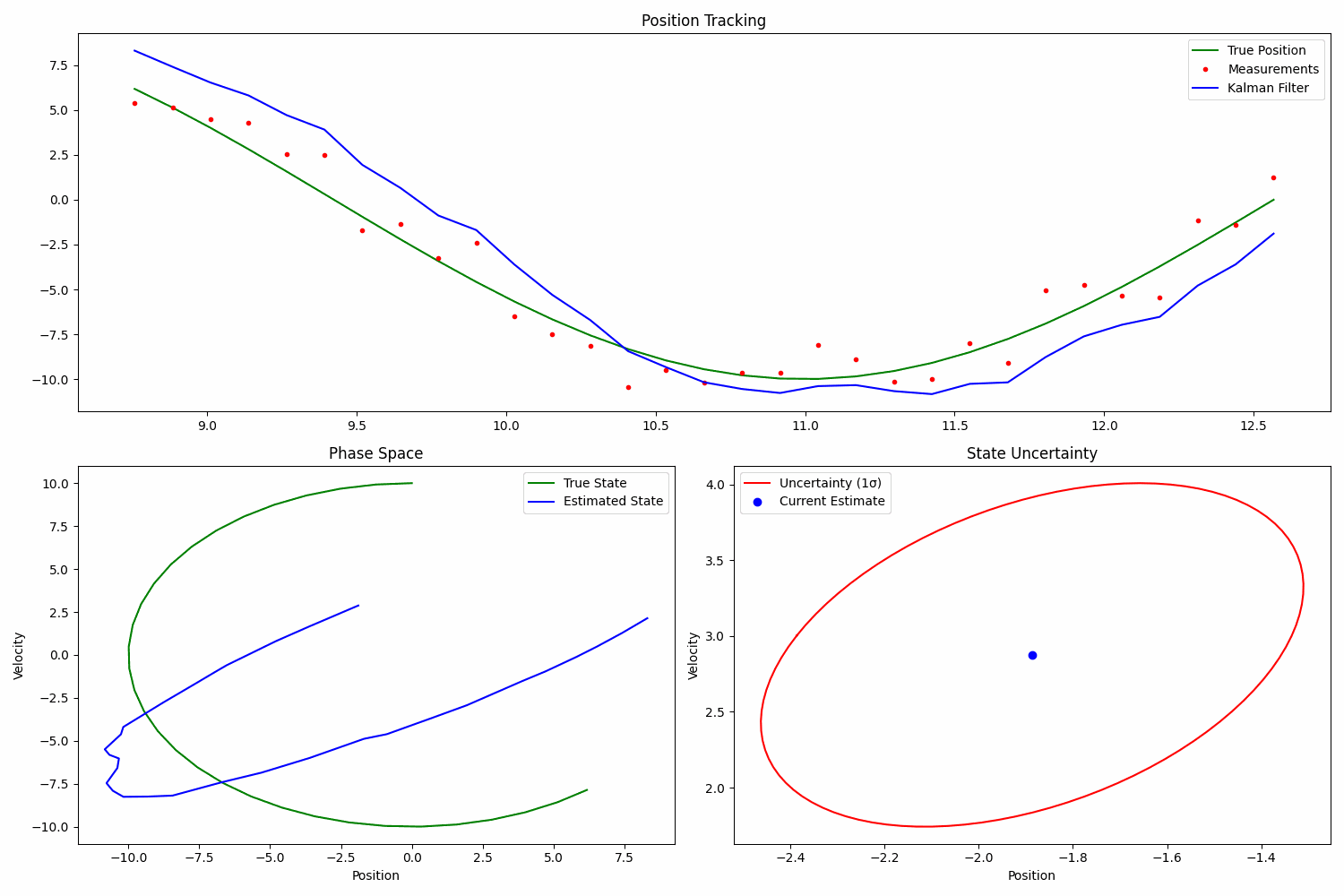
物体追踪是状态估计技术的一个简单现实世界示例。在此示例中，物体的真实运动遵循可预测的正弦模式，但由于传感器测量中的噪声，我们追踪它的能力变得复杂，这使其成为展示滤波器性能的绝佳案例。

该系统可以使用状态空间方程进行建模，其中状态向量包括位置和速度分量。正弦轨迹提供了一个自然的测试用例，因为它涉及位置和速度的连续变化，这对滤波器保持准确追踪的能力提出了挑战。状态转移模型必须考虑潜在的正弦动力学，而测量模型则反映传感器中带有噪声的位置观测值。

该追踪系统的实现通常展示了滤波器如何有效地去除测量噪声，并提供物体真实位置和速度的平滑估计。此示例特别突出了滤波器在测量值存在噪声或间歇时仍能保持追踪准确性的能力，使其成为状态估计原理在实际应用中的有价值的演示。通过绘制真实轨迹、带噪声的测量值和滤波估计值，可以直观地看到滤波器的性能，清晰地展示了滤波器如何在保持准确追踪的同时平滑测量噪声。

def generate_trajectory(n_steps, noise_std=0.1):
    """Generate a noisy trajectory"""
    t = np.linspace(0, 4 * np.pi, n_steps)
    true_position = 10 * np.sin(t)
    true_velocity = 10 * np.cos(t)
    true_states = np.vstack((true_position, true_velocity))
    measurements = true_position + np.random.normal(0, noise_std, n_steps)
    return true_states, measurements
def track_object():
    # Generate data
    n_steps = 100
    true_states, measurements = generate_trajectory(n_steps)
    # Initialize model and filter
    model = StateSpaceModel(state_dim=2, observation_dim=1)
    model.F = np.array([[1, 1], [0, 1]])  # Position and velocity
    kf = KalmanFilterCustom(model)
    # Run filter
    estimated_states = []
    for measurement in measurements:
        kf.predict()
        est_state, _ = kf.update(measurement)
        estimated_states.append(est_state)
    return np.array(estimated_states), true_states, measurements
# Execute tracking
estimated_states, true_states, measurements = track_object()

非线性系统的高级滤波器

扩展卡尔曼滤波器（EKF）在当前状态估计值附近对非线性模型进行线性化，从而使得卡尔曼滤波器原理能够应用于非线性系统。EKF通过使用泰勒级数展开进行局部线性化，并计算雅可比矩阵（偏导数）以在当前工作点创建线性近似。此过程包括两个主要步骤：预测，其中使用非线性模型预测未来状态；更新，其中使用线性化模型进行卡尔曼更新方程的计算。

EKF应用于导航系统、机器人定位、目标追踪、过程控制以及金融建模等领域。其处理非线性系统的能力，同时保持相对高效的计算，使其成为许多实际应用中的实用选择。

class ExtendedKalmanFilter:
    def __init__(self, f, h, q_dim, r_dim):
        self.f = f  # State transition function
        self.h = h  # Measurement function
        self.Q = np.eye(q_dim) * 0.1
        self.R = np.eye(r_dim) * 1.0
def predict(self, x, P):
        x_pred = self.f(x)
        F = self.numerical_jacobian(self.f, x)
        P_pred = F @ P @ F.T + self.Q
        return x_pred, P_pred
    def update(self, x_pred, P_pred, measurement):
        H = self.numerical_jacobian(self.h, x_pred)
        y = measurement - self.h(x_pred)  # Innovation
        S = H @ P_pred @ H.T + self.R
        K = P_pred @ H.T @ np.linalg.inv(S)  # Kalman gain
        x = x_pred + K @ y
        P = (np.eye(len(x)) - K @ H) @ P_pred
        return x, P
    @staticmethod
    def numerical_jacobian(func, x, eps=1e-7):
        n = len(x)
        J = np.zeros((n, n))
        for i in range(n):
            x_plus = x.copy()
            x_plus[i] += eps
            J[:, i] = (func(x_plus) - func(x)) / eps
        return J

无迹卡尔曼滤波器（UKF）通过精心选择的西格玛点来估计和传递系统状态经过非线性变换后的均值和协方差，从而避免了扩展卡尔曼滤波器（EKF）所需的显式雅可比矩阵计算。UKF的工作原理是在当前状态估计值周围选择一组样本点（西格玛点），将这些点通过非线性系统进行传递，然后从传递后的点中重构变换后的均值和协方差。此过程包括两个主要步骤：通过非线性模型生成和传递sigma点，以及从变换后的点中重构统计特性。

UKF的应用领域与EKF相似，包括导航、目标追踪和自动驾驶车辆的状态估计，但在非线性较强的系统中，UKF往往表现更好。UKF能够捕捉更高阶的统计矩，同时保持合理的计算复杂度，这使得它在许多现代应用中越来越受青睐，相较于EKF更具优势。

from filterpy.kalman import UnscentedKalmanFilter, MerweScaledSigmaPoints.kalman import UnscentedKalmanFilter, MerweScaledSigmaPoints
def initialize_ukf(dim_x, dim_z, fx, hx):
    points = MerweScaledSigmaPoints(dim_x, alpha=0.1, beta=2.0, kappa=-1)
    ukf = UnscentedKalmanFilter(dim_x=dim_x, dim_z=dim_z, dt=1.0, fx=fx, hx=hx, points=points)
    ukf.Q = np.eye(dim_x) * 0.1
    ukf.R = np.eye(dim_z) * 1.0
    return ukf

实际应用与可视化

以下是如何对卡尔曼滤波器的结果进行可视化：

import matplotlib.pyplot as plt.pyplot as plt
def visualize_results(true_states, measurements, estimated_states):
    plt.figure(figsize=(12, 6))
    plt.plot(true_states[0], label="True Position")
    plt.plot(measurements, 'r.', label="Measurements")
    plt.plot(estimated_states[:, 0], 'g-', label="Estimated Position")
    plt.title("Kalman Filter Tracking")
    plt.legend()
    plt.grid(True)
    plt.show()
# Visualize
visualize_results(true_states, measurements, estimated_states)

在选择和实施状态估计滤波器时，关键考虑因素在于使滤波器类型与系统特性和噪声性质相匹配。对于具有高斯噪声的线性系统，标准卡尔曼滤波器提供了最优估计。然而，非线性系统需要更高级的方法，如扩展卡尔曼滤波器（EKF）或无迹卡尔曼滤波器（UKF），而具有非高斯噪声分布的系统则最好通过粒子滤波器来处理。这种系统化的模型选择方法确保了给定应用中最有效的估计策略。

参数调整是滤波器实施的关键部分，特别需要注意过程噪声协方差（Q）和测量噪声协方差（R）矩阵。这些参数对滤波器性能有显著影响，必须仔细校准以反映实际的系统和测量不确定性。Q表示系统模型的不确定性，而R表示传感器测量的不确定性。

性能评估通常依赖于均方根误差（RMSE）等指标，该指标量化了估计状态与真实状态之间的差异。RMSE提供了一种标准化的方法来评估滤波器准确性并比较不同的实现方案，帮助工程师优化其滤波器设计并确保可靠的状态估计。在滤波器开发的测试和验证阶段，这一指标尤其有价值。

结论

状态空间模型和卡尔曼滤波是时间序列分析的强大工具，为噪声测量和隐藏状态提供了稳健的解决方案。无论是处理线性系统还是非线性系统，理解准确性、复杂性和计算需求之间的权衡对于成功实施至关重要。