sakana.ai最新研究论文背后的理念是适应性，该论文为新型Transformer架构提供了一个通用框架。就像那个一有外人在场就变成甜心的有毒伴侣一样，大型语言模型（LLM）需要适应各种任务，才能适用于特定领域的使用。

然而，传统的大型语言模型（LLM）后训练存在几个缺点：

• 微调资源消耗巨大：即使采用混合精度、量化和参数高效微调（PEFT）等现代技术，微调LLM的过程仍然非常昂贵，需要大量的计算和存储资源。
• 过拟合问题：很多时候，微调后的模型开始生成重复的输出，并且容易遭受灾难性遗忘。
• 任务干扰：相互冲突的梯度通常会导致模型在某一特定任务上表现更好，而在另一任务上的性能却下降。

自适应LLM

我们将自适应LLM定义为一类能够根据环境变化动态调节其行为，而无需任何外部干预的模型。

如何实现这种智能模型呢？

改进现有LLM-我们都熟悉LLM的扩展定律和涌现能力，因此，如果我们继续创建更大的模型，它们显然会在多种任务上表现更好，并在多个领域产生不错的输出。然而，这并不是一个非常有可扩展性的想法，并且需要大量的计算能力。

使用混合专家（MoE）模型-MoE的思想是动态地将输入路由到专门处理特定领域的“专家”模块。作者提出，Transformer²可以大致归类为MoE模型，但在重要方面有所不同。

去年，麻省理工学院和乔治亚理工学院发表了一篇题为“Self-MoE：迈向具有自我专业化专家的组合式大型语言模型”的论文，介绍了一种将单体LLM转换为组合式系统的方法。其思想是——不是使用人工标注的数据（如MoE中的情况），而是使用合成数据从头开始创建单个专家模块。然后，这些模块由基础LLM共享，基础LLM将特定输入路由到特定模块。

自适应LLM的好处包括：

• 为不同任务动态修改模型，而无需反复微调。
• 持续学习，随着时间的推移，模型可以积累信息，而不是用静态信息进行训练。
• 消除灾难性遗忘，可以向模型中添加新信息，而不会触发任何形式的灾难性遗忘，即模型在学习新任务后忘记如何执行先前任务。

作者还强调，自适应LLM模仿了神经科学原理，即“根据当前任务激活大脑的特定区域”。

虽然MoE是创建组合式系统的绝佳方式，但为每个单独任务训练一个单独的“专家”模块仍然是一种资源密集型方法。为了解决这个问题，论文介绍了一种新颖的微调技术——奇异值微调（Singular Value Fine-Tuning，SVF）。

奇异值微调

在深入探讨论文作者使用的技术之前，让我们先了解一下理解这种方法所需的一些基本概念。

使用奇异值分解（SVD）进行微调

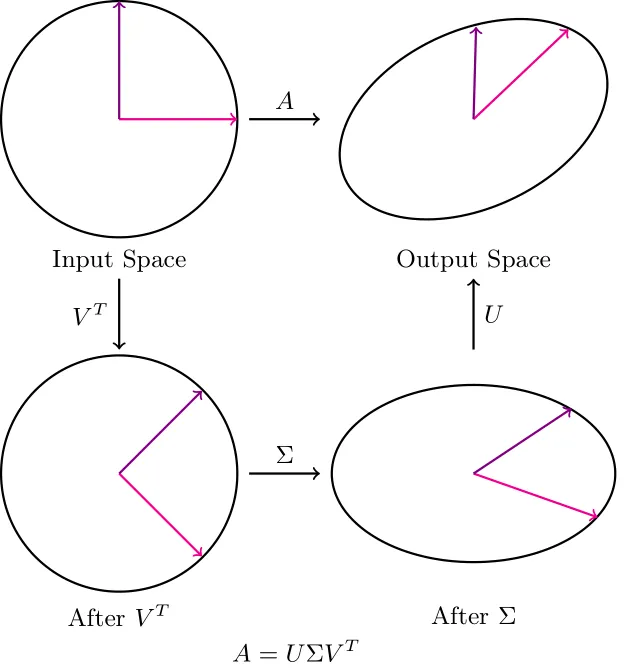
在SVD中，U和V都对向量空间进行旋转。我们这里关注的重点是Σ矩阵。

注意到当Σ按其对应的奇异值对向量进行缩放时，基向量与主轴（最大方差的方向）对齐。因此，改变缩放值可以被看作是在改变我们给予特定主轴的权重。改变缩放值可以被看作是在调整我们给予特定主轴的重视程度。

由于这些奇异值可以近似表示不同“特征”的“重要性”，我们可以忽略V和U的变化。

因此，在微调网络时，我们只更新权重矩阵的奇异值，这导致需要训练的参数数量呈指数级减少。

这种方法的唯一缺点是，当我们只训练前k个奇异值时，可能会有一些信息损失（取决于不同方向上方差的均匀程度）。

基于SVD的微调与LoRA的比较

加载模型，

from transformers import AutoModelForCausalLM, AutoTokenizer
name = "Qwen/Qwen2.5-1.5B-Instruct"
model = AutoModelForCausalLM.from_pretrained(name)
tokenizer = AutoTokenizer.from_pretrained(name)

使用LoRA时，看看可训练参数的数量。

from peft import LoraConfig, peft_model
lora_config = LoraConfig(
    task_type="CAUSAL_LM",
    r=8,
    lora_alpha=32,
    lora_dropout=0.1,
    bias="none",
)
lora_model = peft_model.get_peft_model(model, lora_config)
lora_model.print_trainable_parameters()

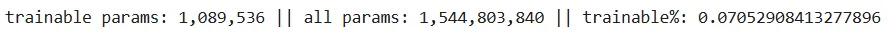
当使用SVD（更新全部三个矩阵——U、V和Σ）时，看看可训练参数的数量。

# SVD
from svd_training.svd_model import SVDForCausalLM
  
svd_model = SVDForCausalLM.create_from_model(model, rank_fraction=0.1)
print(f"trainable params: {svd_model.num_parameters(only_trainable=True)} || all params: {svd_model.num_parameters()} || trainable%: {svd_model.num_parameters(only_trainable=True) / svd_model.num_parameters()}")

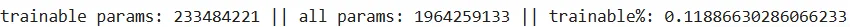
显然，使用基于SVD的微调时，可训练参数的数量更多，这是为什么呢？其实答案在于，我们不仅仅是在更新奇异值，而是在更新分解后的矩阵中的所有值。

以下是应用SVD分解后模型的样子：

Qwen2ForCausalLM(
  (model): Qwen2Model(
    (embed_tokens): Embedding(151936, 1536)
    (layers): ModuleList(
      (0-27): 28 x Qwen2DecoderLayer(
        (self_attn): Qwen2SdpaAttention(
          (q_proj): SVDLinear()
          (k_proj): SVDLinear()
          (v_proj): SVDLinear()
          (o_proj): SVDLinear()
          (rotary_emb): Qwen2RotaryEmbedding()
        )
        (mlp): Qwen2MLP(
          (gate_proj): SVDLinear()
          (up_proj): SVDLinear()
          (down_proj): SVDLinear()
          (act_fn): SiLU()
        )
        (input_layernorm): Qwen2RMSNorm()
        (post_attention_layernorm): Qwen2RMSNorm()
      )
    )
    (norm): Qwen2RMSNorm()
  )
  (lm_head): SVDLinear()
)

让我们来做一些计算。模型有28个解码器层，每个解码器层有7个SVD线性层。此外，还有一个模型头部，也被转换成了SVD线性层。因此，总共有：

28 * 7 + 1 = 197个SVD线性层

如果我们只让Σ矩阵中的奇异值可训练，而保持其他部分冻结，那么每个SVD线性层有1536个奇异值。因此，总的奇异值数量为：

1536 * 197 = 302,592个奇异值

这是在奇异值微调中将要训练的有效参数数量，相当于LoRA所使用参数数量的0.00129%。

类似的工作在去年发表的LoRA-XS论文中也做过。然而，这项工作引入了强化学习来提高学习效率。

接下来是论文最重要的贡献：Transformer²

该框架被分解为两个关键步骤：

• 使用SVF（奇异值微调）基于基础模型权重的SVD（奇异值分解）学习紧凑且组合式的强化学习专家向量。（下图左侧）
• 三种适应策略，在推理过程中结合这些专家向量。（下图右侧）

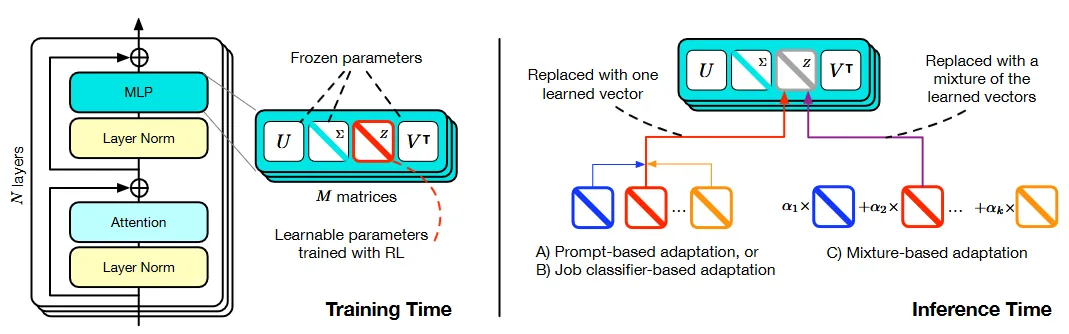
在这篇文章的前面部分，我们查看了大量代码来理解奇异值微调（SVF）。现在，让我们来看看这些专家向量是如何通过强化学习（RL）进行训练的。我们之前已经了解到，只需要更新Σ矩阵。数学上，我们可以说，

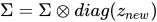
其中z是奇异值微调（SVF）专家向量。

然后，论文中的作者使用了带有单一奖励和KL惩罚（用于偏离原始模型行为）的REINFORCE算法。这种方法有助于创建更好的“专家”向量，并放宽了对数据集必须庞大的约束。

这些专家向量的一大优点是它们提供的高度组合性。这些向量具有高度的可解释性，并且可以进行代数操作。

自适应部分是如何工作的？

该框架定义了一种两阶段适应策略，结合了K组基础“专家”向量。

• 第一阶段推理：给定一个任务，观察模型的测试行为，并创建一个z'向量，该向量封装了这一行为。
• 第二阶段推理：使用这个适应后的向量z'来生成实际响应。

其思路是，通过观察测试时的行为，模型可以适应并包含其可用的专家向量的任何线性组合，以生成最终输出。

结论

虽然论文确实讨论了一种构建自适应大型语言模型（LLM）的创新方法，但创建专家SVF向量的过程比使用单独模块（如在LoRA中）更复杂。此外，参数高效微调（PEFT）技术有大量库支持，这使得最终用户的使用更简单。然而，如果你对权重矩阵的样子以及如何操作它们有深入的理解，那么SVF绝对值得一看。