我们正在寻找不同时间间隔内时间序列数据中的模式。例如，股票市场价格在危机期间可能表现出高波动性，而在稳定时期则表现出低波动性。制度转换模型通过假设时间序列在不同“制度”之间切换来帮助识别这种行为，每种制度都有其自身的统计特性。

在本文中，我们将探讨制度转换模型、其应用以及如何使用Python中的statsmodels库来实现它们。

什么是制度转换模型？

制度转换模型由詹姆斯·汉密尔顿于1989年提出，通过允许在不同状态或制度之间转换来捕捉时间序列数据中的结构性变化。这些模型在以下领域特别有用：

1. 经济学：建模经济衰退和扩张。
2. 金融学：分析牛市和熊市。
3. 能源领域：检测需求或生产趋势的转变。
4. 天气学：捕捉气候状态之间的转换。

最常见的制度转换模型是马尔可夫转换模型，其中制度转换遵循马尔可夫过程。

马尔可夫链和状态依赖概率

马尔可夫转换模型就像一个讲述多个版本相同故事的说书人。想象一下，一个经济体在繁荣期和萧条期之间切换。在任何时刻，经济体都会根据它当前是处于繁荣期（状态A）还是萧条期（状态B）而遵循特定的模式。

这种“魔法”是通过马尔可夫链实现的，其中下一个状态仅取决于当前状态，而不是过去。这就像天气预报一样——明天的天气主要取决于今天的条件，而不是上周发生了什么。状态之间转换的概率（转移概率）对于每个当前状态是固定的。例如，在繁荣期，可能有90%的概率继续保持繁荣，10%的概率转为萧条。

在每个状态内，结果遵循特定于状态的概率分布（状态依赖概率）。在繁荣期，增长可能平均为3%，波动性较低，而在萧条期，增长可能平均为-1%，波动性较高。该模型结合了这些要素（制度识别、转移概率和特定于状态的行为）来捕捉数据中的复杂模式。

statsmodels库通过其MarkovRegression和MarkovAutoregression类提供了马尔可夫转换模型的便捷实现。让我们通过一个示例来逐步了解。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.regime_switching.markov_regression import MarkovRegression
import seaborn as sns
from scipy import stats

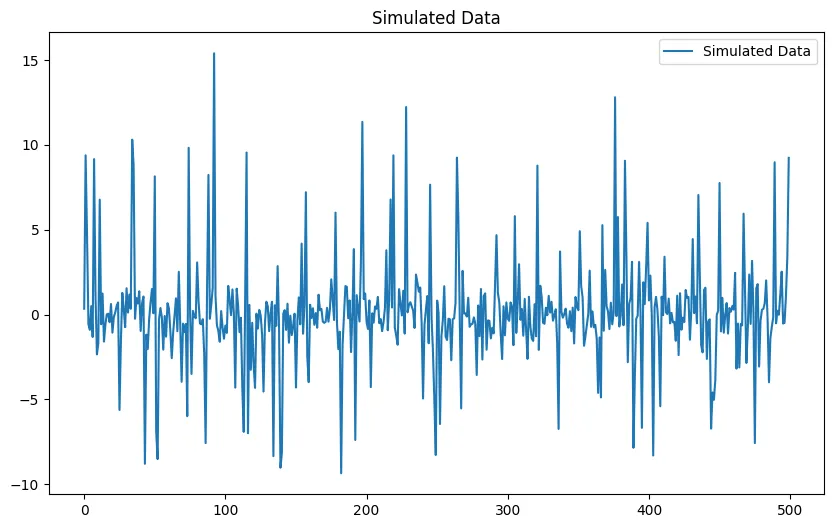
我们将生成具有两种制度（高波动性和低波动性）的合成数据。

# Generate and prepare data
np.random.seed(42)
n = 500
regimes = np.random.choice([0, 1], size=n, p=[0.7, 0.3])
data = np.array(np.random.normal(0, np.where(regimes == 0, 1, 5)))
# 2. Create a DataFrame with all the information
df = pd.DataFrame({
    'Data': data,
    'True_Regime': regimes,
    'Time': range(n)
})

# Fit a Markov switching model
model = MarkovRegression(data, k_regimes=2, trend='c', switching_variance=True)
result = model.fit()
print(result.summary())
print("\nTransition Matrix:")
print(result.regime_transition)

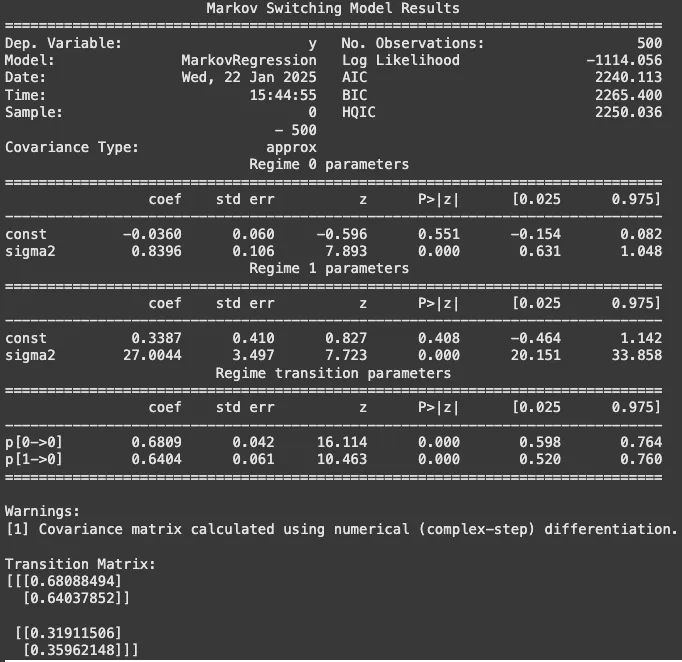
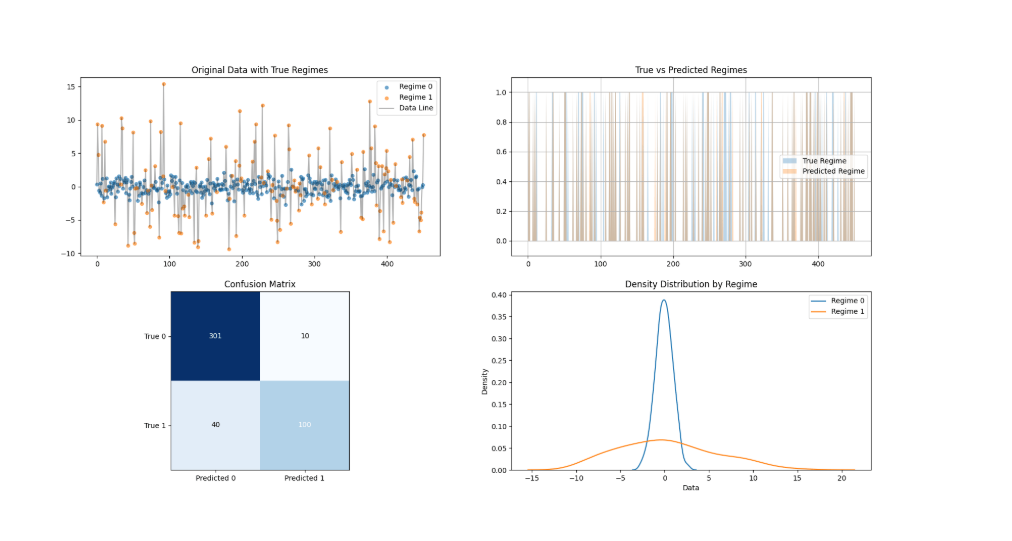
现在，我们有了每个点的实际值和预测值。

# Add predicted probabilities and regimes to DataFrame
df['Predicted_Prob_High'] = result.smoothed_marginal_probabilities[:, 1]
df['Predicted_Regime'] = np.argmax(result.smoothed_marginal_probabilities, axis=1)
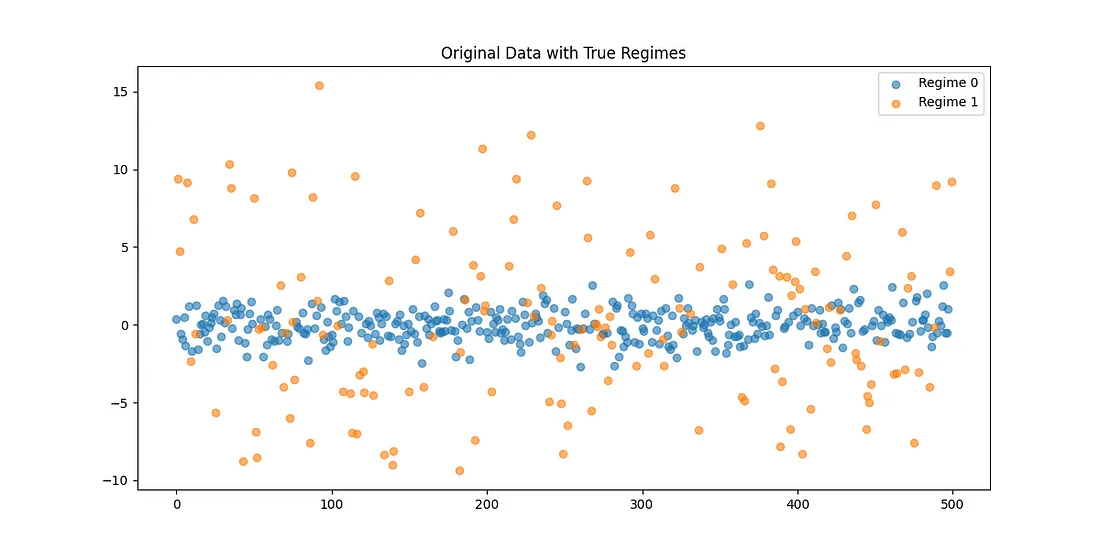
# Plot 1: Original Data with Regime Highlighting
plt.figure(figsize=(12, 6))
for regime in [0, 1]:
    mask = df['True_Regime'] == regime
    plt.scatter(df[mask]['Time'], df[mask]['Data'], 
                label=f"Regime {regime}", alpha=0.6)
plt.title("Original Data with True Regimes")
plt.legend()
plt.savefig('original_data_regimes.png')
plt.close()

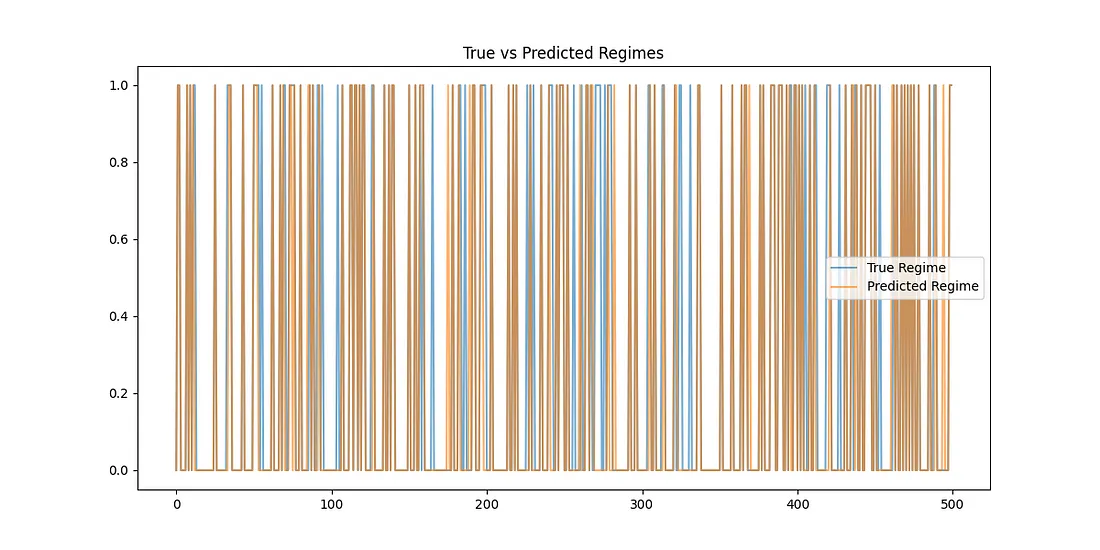
# Plot 2: Predicted vs True Regimes2: Predicted vs True Regimes
plt.figure(figsize=(12, 6))
plt.plot(df['True_Regime'], label='True Regime', alpha=0.6)
plt.plot(df['Predicted_Regime'], label='Predicted Regime', alpha=0.6)
plt.title("True vs Predicted Regimes")
plt.legend()
plt.savefig('true_vs_predicted_regimes.png')
plt.close()

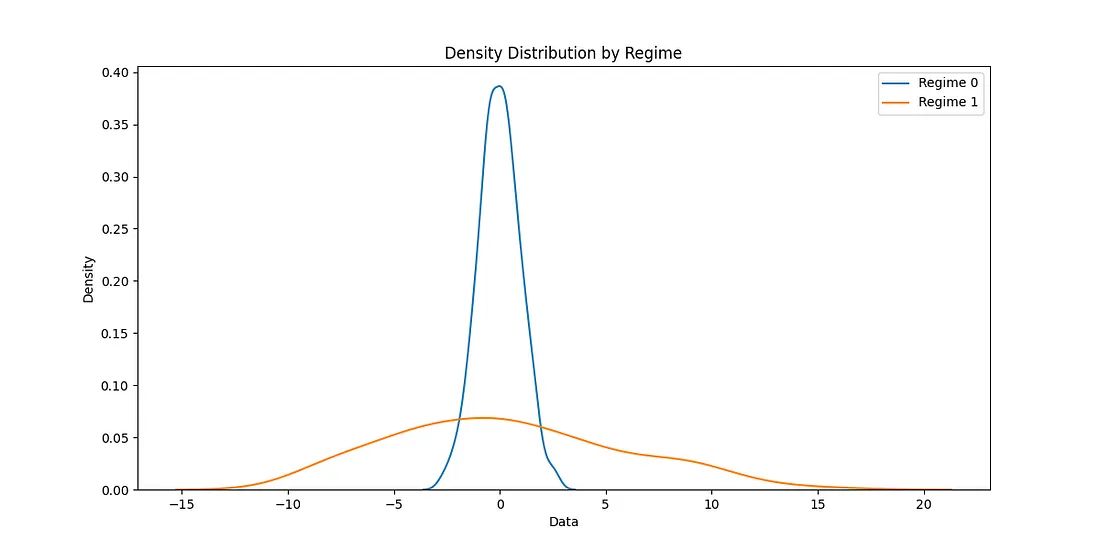
# Plot 3: Density Plot for Each Regime3: Density Plot for Each Regime
plt.figure(figsize=(12, 6))
for regime in [0, 1]:
    sns.kdeplot(data=df[df['True_Regime'] == regime]['Data'], 
                label=f"Regime {regime}")
plt.title("Density Distribution by Regime")
plt.legend()
plt.savefig('density_distribution.png')
plt.close()

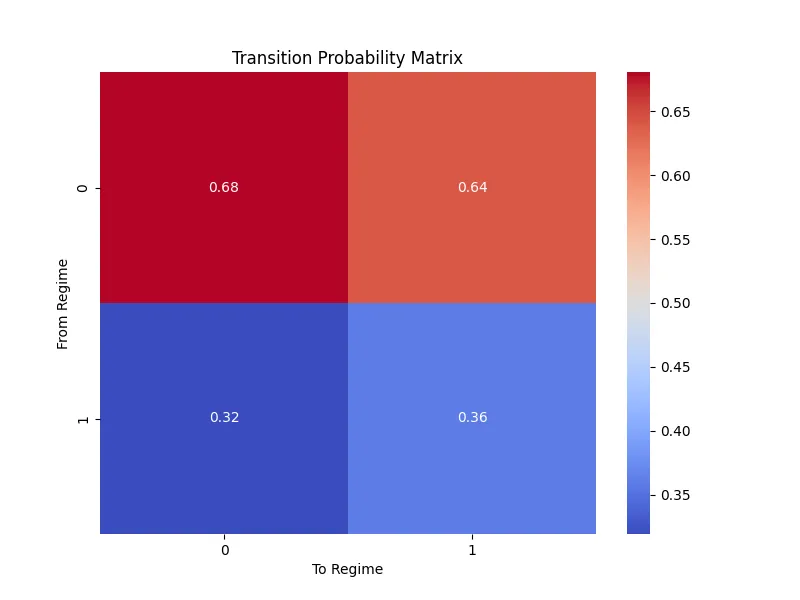
# Plot 4: Transition Probability Matrix Heatmap
plt.figure(figsize=(8, 6))
transition_matrix = result.regime_transition.reshape(2, 2)
sns.heatmap(transition_matrix, annot=True, cmap='coolwarm')
plt.title("Transition Probability Matrix")
plt.xlabel("To Regime")
plt.ylabel("From Regime")
plt.savefig('transition_matrix.png')
plt.close()

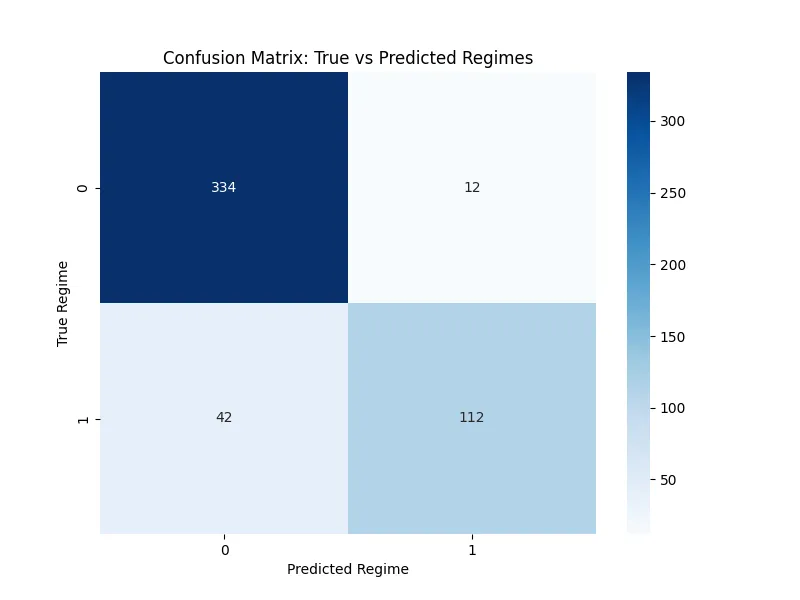
# Plot 5: Model Performance Metrics5: Model Performance Metrics
plt.figure(figsize=(8, 6))
confusion_matrix = pd.crosstab(df['True_Regime'], df['Predicted_Regime'])
sns.heatmap(confusion_matrix, annot=True, fmt='d', cmap='Blues')
plt.title("Confusion Matrix: True vs Predicted Regimes")
plt.xlabel("Predicted Regime")
plt.ylabel("True Regime")
plt.savefig('confusion_matrix.png')
plt.close()

# Print Statistics
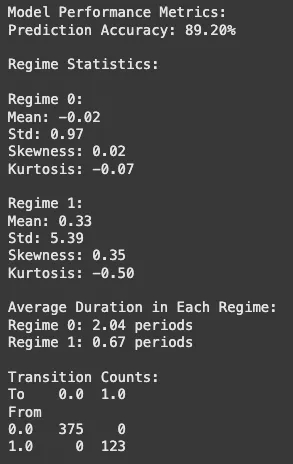
print("\nModel Performance Metrics:")
accuracy = (df['True_Regime'] == df['Predicted_Regime']).mean()
print(f"Prediction Accuracy: {accuracy:.2%}")
print("\nRegime Statistics:")
for regime in [0, 1]:
    regime_data = df[df['True_Regime'] == regime]['Data']
    print(f"\nRegime {regime}:")
    print(f"Mean: {regime_data.mean():.2f}")
    print(f"Std: {regime_data.std():.2f}")
    print(f"Skewness: {stats.skew(regime_data):.2f}")
    print(f"Kurtosis: {stats.kurtosis(regime_data):.2f}")
print("\nAverage Duration in Each Regime:")
for regime in [0, 1]:
    regime_runs = (df['Predicted_Regime'] == regime).astype(int).groupby(
        (df['Predicted_Regime'] != df['Predicted_Regime'].shift()).cumsum()
    ).sum()
    print(f"Regime {regime}: {regime_runs.mean():.2f} periods")
# Calculate and print transition statistics
transitions = pd.DataFrame({
    'From': df['Predicted_Regime'][:-1],
    'To': df['Predicted_Regime'][1:]
})
print("\nTransition Counts:")
print(pd.crosstab(transitions['From'], transitions['To']))

实际考虑因素

与其他时间序列模型一样，在拟合制度转换模型之前，我们需要确保数据是平稳的。我们可以使用迪基-富勒检验（Dickey-Fuller）或KPSS检验来测试数据的平稳性。此外，我们还需要根据领域知识或使用阈值（如最大化赤池信息准则（AIC））来确定我们认为数据中存在的制度数量。

结论

制度转换模型为分析具有结构变化的时间序列提供了一个灵活的框架。它们可以帮助我们发现传统模型可能忽略的见解。使用Python和statsmodels，你可以高效地实现这些模型，并根据你的特定需求进行适应。

特定于制度的模型可以提高预测的准确性，用于预测。它们可以用于发现时间序列行为中的显著变化，用于变点检测。

制度转换还可以用于时间序列分类或聚类任务的特征工程，为进一步的机器学习工作准备数据。