本文主要讲解多头潜在注意力机制（Multi-head Latent Attention），该机制在DeepSeek-V2开发过程中首次提出，并在DeepSeek-V3中得到运用。

为了更好地理解 MLA 并使本文具有独立性，在深入讨论 MLA 的细节之前，我们将在本节中重新讨论几个相关概念。

仅解码器的 Transformer 中的 MHA

请注意，MLA 是为了加快自回归文本生成中的推理速度而开发的，因此我们在这种情况下讨论的 MHA 适用于仅解码器的 Transformer。

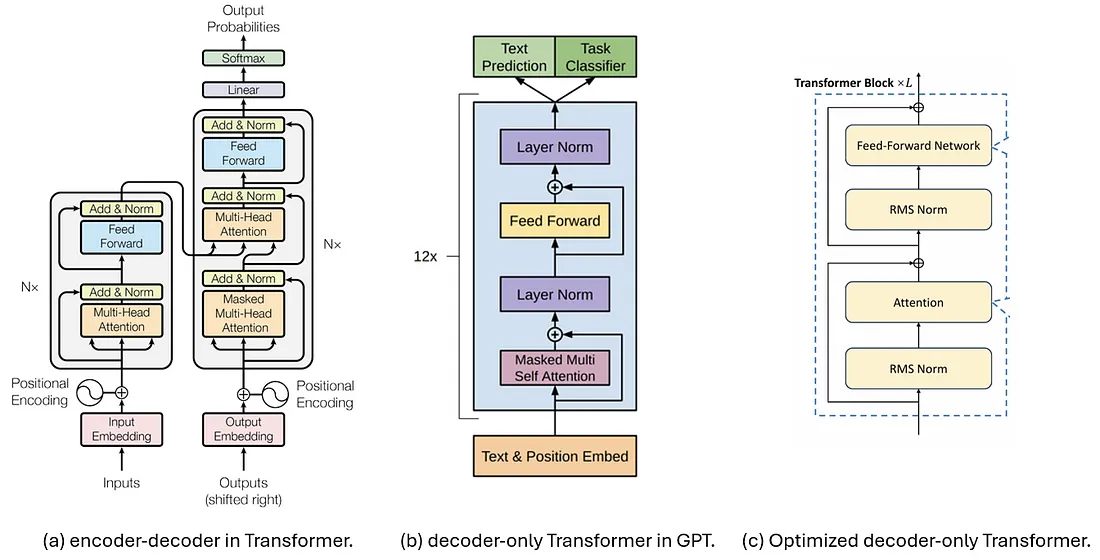
下图比较了三种用于解码的 Transformer 架构，其中 (a) 展示了原始“Attention is All You Need”论文中提出的编码器和解码器。其解码器部分随后被简化，从而产生了 (b) 所示的仅包含解码器的Transformer模型，该模型后来被用于GPT等许多生成模型中。

如今，LLM 更常见的是选择 (c) 所示的结构，以便进行更稳定的训练，其中对输入而不是输出应用归一化，并将 LayerNorm 升级为 RMS Norm。这将作为我们在本文中讨论的基准架构。

在此背景下，MHA 计算基本遵循中的流程，如下图所示：

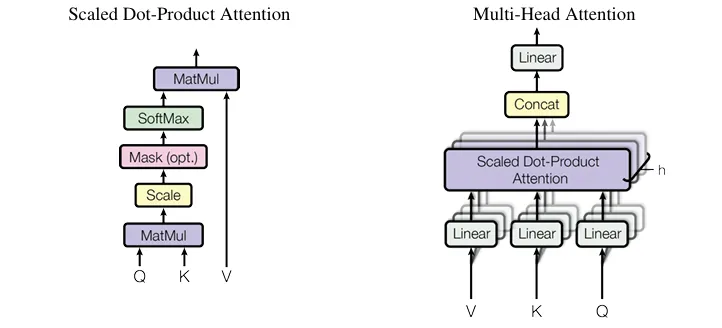
假设我们有n_h 个注意力头，每个注意力头的维度表示为d_h，因此连接后的维度为 ( n_h · d_h )。

给定一个具有l层的模型，如果我们将该层中第 t 个 token 的输入表示为维度为d 的h_t，则我们需要使用线性映射矩阵将h_t的维度从d映射到 ( h_n · d_h )。

更正式地，我们有：

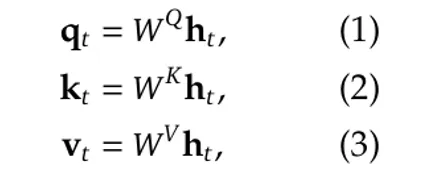
其中W^Q、W^K和W^V是线性映射矩阵：

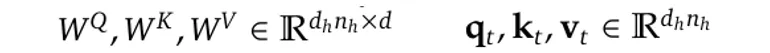
经过这样的映射，q_t，k_t和v_t将被拆分成n_h个头，以计算缩放的点积注意力：

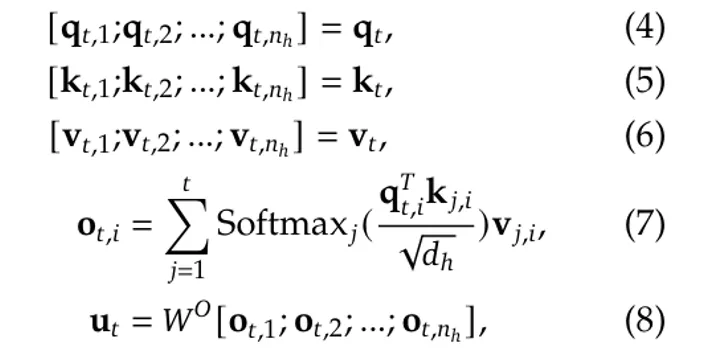
其中W^O是另一个投影矩阵，用于将维度从 ( h_n · d_h ) 逆映射到d：

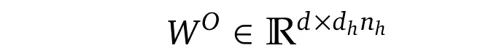
注意，上面的公式（1）到（8）描述的只是针对单个 token 的，在推理过程中，我们需要对每个新生成的 token 重复这个过程，这涉及到大量的重复计算，这就引出了一种叫做 Key-Value 缓存的技术。

键值缓存

顾名思义，键值缓存是一种通过缓存和重用以前的键和值来加速自回归过程的技术，而不是在每个解码步骤中重新计算它们。

请注意，KV 缓存通常仅在推理阶段使用，因为在训练中我们仍然需要并行处理整个输入序列。

KV 缓存通常实现为滚动缓冲区。在每个解码步骤中，仅计算新的查询 Q，而缓存中存储的 K 和 V 将被重用，以便使用新的 Q 和重用的 K、V 来计算注意力。同时，新的 token 的 K 和 V 也会附加到缓存中以供后续使用。

然而，KV 缓存实现的加速是以内存为代价的，因为 KV 缓存通常会随着批次大小 × 序列长度 × 隐藏大小 × 头数量而扩展，当我们有更大的批次大小或更长的序列时会导致内存瓶颈。

多查询注意力 (MQA) 与分组查询注意力 (GQA)

下图是原始 MHA、Grouped-Query Attention (GQA) 和 Multi-Query Attention (MQA) 的比较。

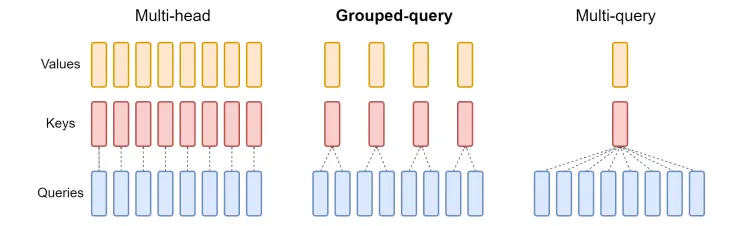
MQA 的基本思想是在所有查询头之间共享单个键和单个值头，这可以显著减少内存使用量，但也会影响注意力的准确性。

GQA 可以看作是 MHA 和 MQA 之间的一种插值方法，其中一对键和值头仅由一组查询头共享，而不是所有查询。但与 MHA 相比，这仍然会导致较差的结果。

RoPE（旋转位置嵌入）

我们需要提及的最后一点背景是 RoPE，它通过使用正弦函数旋转多头注意力中的查询和键向量，将位置信息直接编码到注意力机制中。

更具体地说，RoPE 将位置相关的旋转矩阵应用于每个标记处的查询和键向量，并使用正弦和余弦函数作为其基础，但以独特的方式应用它们来实现旋转。

要了解是什么使其与位置相关，请考虑一个仅具有 4 个元素的玩具嵌入向量，即 (x_1、x_2、x_3、x_4)。

为了应用 RoPE，我们首先将连续的维度分组为：

• x_1，x_2）->位置 1
• （x_3，x_4）->位置 2

然后，我们应用旋转矩阵来旋转每一对：

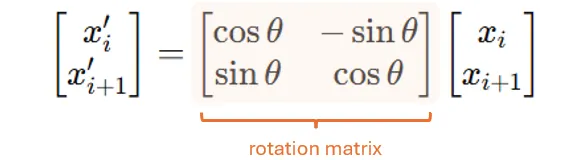
其中 θ = θ(p) = p ⋅ θ_0​，θ_0​ 是基频。在我们的 4 维玩具示例中，这意味着 (x_1, x_2) 将旋转 θ_0​，而 (x_3, x_4) 将旋转 2 ⋅ θ_0。

这就是为什么我们将这个旋转矩阵称为位置相关的：在每个位置（或每对），我们将应用不同的旋转矩阵，其中旋转角度由位置决定。

RoPE 因其对长序列编码的效率而在现代 LLM 中被广泛使用，但从上面的公式我们可以看出，它对 Q 和 K 都是位置敏感的，这使得它在某些方面与 MLA 不兼容。

多头潜在注意力

最后，我们可以进入 MLA 部分。在本节中，我们将首先概述 MLA 的高层思想，然后深入探讨为什么需要修改 RoPE。最后，我们介绍 MLA 的详细算法及其性能。

MLA：高层次理念

MLA 的基本思想是将注意力输入h_t压缩成一个维度为d_c 的低维隐向量，其中d_c远低于原始的 ( h_n · d_h )。稍后当我们需要计算注意力时，我们可以将这个隐向量映射回高维空间以恢复键和值。这样一来，只需要存储隐向量，从而大大减少内存占用。

这个过程可以用下面的公式更正式地描述，其中c^{KV}_t是潜在向量，W^{DKV}是将h_t的维度从 ( h_n · d_h ) 映射到d_c的压缩矩阵（这里上标中的 D 代表“向下投影”，即压缩维度），而W^{UK}和W^{UV}都是将共享潜在向量映射回高维空间的向上投影矩阵。

类似地，我们还可以将查询映射到潜在的低维向量，然后将其映射回原始的高维空间：

为什么需要解耦 RoPE

正如我们之前提到的，RoPE 是训练生成模型处理长序列的常见选择。如果我们直接应用上述 MLA 策略，这将与 RoPE 不兼容。

为了更清楚地看到这一点，考虑一下当我们使用公式 (7) 计算注意力时会发生什么：当我们将转置的q与k相乘时，矩阵W^Q和W^{UK}将出现在中间，它们的组合等同于从d_c到d 的单个映射维度。

在原始论文中，作者将其描述为W^{UK}可以被“吸收”到W^Q中，因此我们不需要将W^{UK}存储在缓存中，从而进一步减少内存使用量。

然而，当我们考虑图 (4) 中的旋转矩阵时，情况就不再如此了，因为 RoPE 将在W^{UK}的左侧应用一个旋转矩阵，并且该旋转矩阵最终将位于转置的W^Q和W^{UK} 之间。

正如我们在背景部分所解释的那样，这个旋转矩阵是位置相关的，这意味着每个位置的旋转矩阵都是不同的。因此，W^{UK} 不再能被 W^Q 吸收。

为了解决这一冲突，作者提出了所谓的“解耦 RoPE ”，通过引入附加查询向量和共享密钥向量，并仅在 RoPE 过程中使用这些附加向量，同时保持原始密钥与旋转矩阵隔离。

MLA 的整个过程可以总结如下：

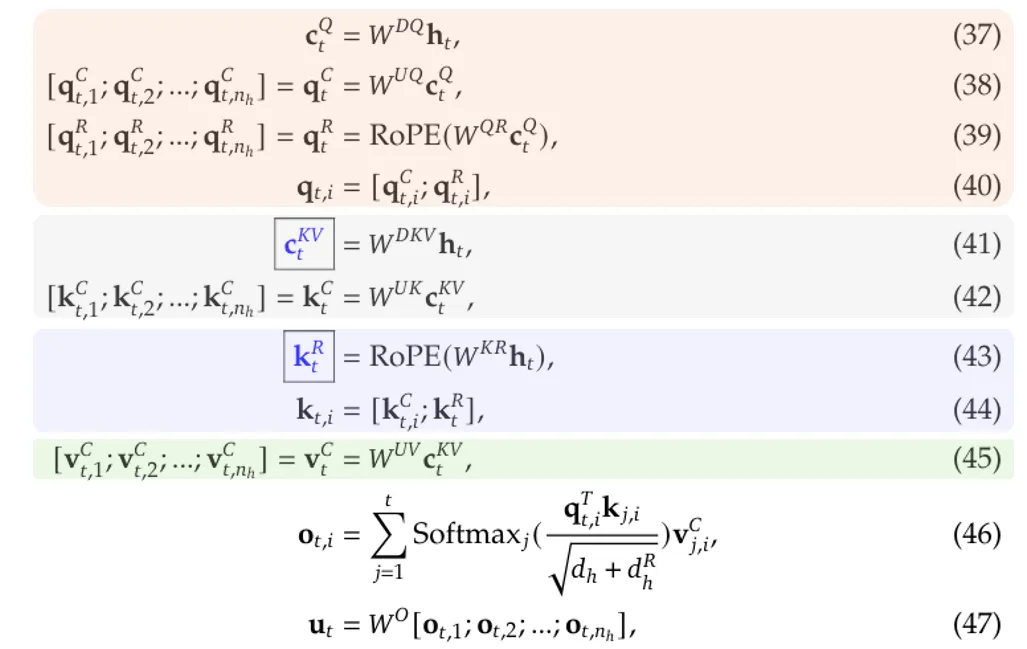
• 等式（37）至（40）描述了如何处理查询标记。
• 公式 (41) 和 (42) 描述了如何处理密钥标记。
• 公式 (43) 和 (44) 描述了如何使用附加共享密钥进行 RoPE，请注意 (42) 的输出不涉及 RoPE。
• 等式（45）描述了如何处理价值标记。

在这个过程中，只有带框的蓝色变量需要被缓存。下面的流程图可以更清楚地说明这个过程：

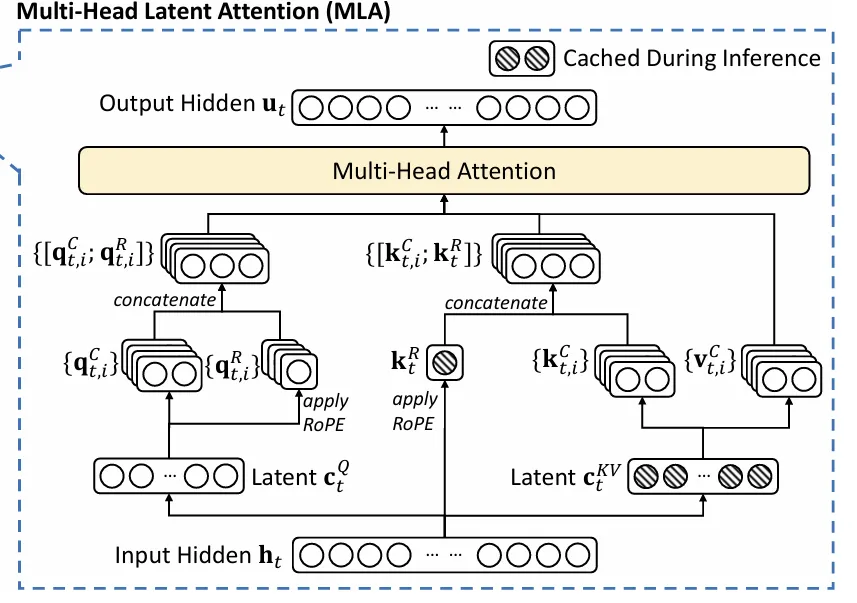
MLA 的履行

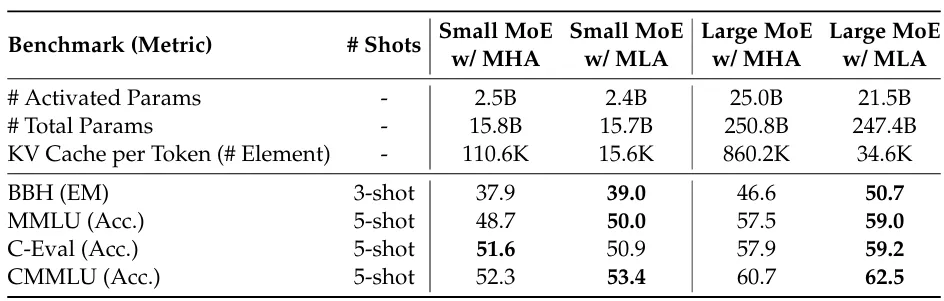
下表比较了 MHA、GQA、MQA 与 MLA 之间每个 token 所需的 KV cache 元素数量以及建模容量，表明 MLA 确实可以在内存效率和建模容量之间取得更好的平衡。

有趣的是，MLA 的建模能力甚至超过了原始的 MHA。

更具体地说，下表显示了 MHA、GQA 和 MQA 在 7B 模型上的性能，其中 MHA 的表现明显优于 MQA 和 GQA。

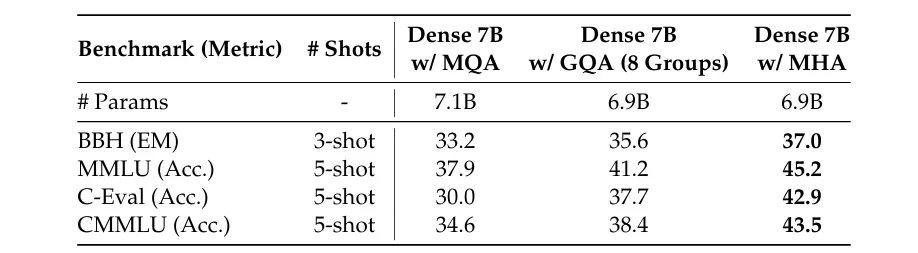
作者还对 MHA 和 MLA 进行了分析，结果总结在下表中，其中 MLA 总体上取得了更好的结果。