当前的大型语言模型无法处理大块的连续文本。主要的瓶颈在于下文所述的注意力模块，该模块将文本处理为单词（或标记）序列。由于注意力的计算成本随序列长度T的平方增长，因此随着文本大小的增加，处理文本的成本变得越来越高。由于注意力是主要的罪魁祸首，人们正在积极探索计算成本更低的替代方案。这些替代方案在架构上各不相同，包括循环（例如，Mamba和xLSTM）、卷积（例如，Hyena ）或基于稀疏性（例如，Longformer [4]和BigBird）。特别是状态空间模型，作为注意力的强大替代方案，正受到越来越多的关注。事实上，基于状态空间模型的大型语言模型（如Mamba 2）在许多任务上的表现与变压器相当甚至更优。除了需要处理长上下文窗口的应用外，状态空间模型还提供了关于注意力与半可分矩阵和状态空间模型之间关系的新见解。

当前基于注意力和状态空间的模型的一个缺点是它们需要大量的训练数据。另一方面，当训练数据稀缺，或者如果你想将一些领域知识融入到模型中时，贝叶斯方法非常有效。此外，与标准的神经网络训练不同，贝叶斯模型不会过度自信，并且允许在未标记数据上进行训练。最后，它们可以提供不确定性水平，这在金融和医疗等高风险应用中非常有用。

在这里，我将介绍一种具有贝叶斯风味的注意力版本，它可以进行序列预测。我们将详细解释如何使用马尔可夫链蒙特卡罗方法训练这个模型。

贝叶斯注意力对我有用吗？

对于更注重实际应用的人来说，以下是一个快速概述，帮助你判断贝叶斯注意力是否适合你的用例。

如果满足以下一个或多个条件，请考虑使用贝叶斯注意力：

• 记录是按顺序排列的（如文本或时间序列）。
• 预测是针对一个或多个连续值（回归）。
• 你的数据集很小，例如只有十几个例子。
• 你的团队有领域知识/启发式方法，你希望将其编码到模型中。
• 预测和模型参数应该具有不确定性意识。
• 你对于每个输出y都有输入变量x。
• 你的一些输出y可能缺失。

变压器回顾

作为复习，我们可以将注意力视为字典查找，其中我们将键k与查询qᵢ进行比较，然后获取对应的值vᵢ。具体来说，使用d个潜在维度

Attn(Q,K,V) = S(QK⊤/√d)V，

其中softmax函数定义为S(x) = [exp[x₁]/Z, exp[x₂]/Z, ...]，Z是配分函数（即归一化常数）。在自注意力中，权重矩阵W，对应于键K = W(k)x、查询Q = W(q)x和值V = W(v)x，都来自相同的输入序列x（但每个都有自己的矩阵，如括号中所示）。关键的是，项QK⊤的形状为T × T，导致了其二次计算成本。然而，事实证明，我们可以摒弃softmax激活函数，并使用核技巧使其线性化。本质上，这个技巧归结于这样一个事实：exp[xy]可以泰勒展开并重写为内积：

exp[xy] = ?(x)·?(y)，

其中?(x) = [1, x, x²/√2, x³/√6, ...]。这样看来，注意力只是一个线性变换

Attn(Q',K',V') = Q'K'⊤V'，

在适当选择的线性基?(Q) -> Q'中定义，该基由核函数?决定。

状态空间模型简介

状态空间模型是一阶微分方程，描述了系统y(t)对给定输入V(t)的响应。例如，状态空间模型用于描述电路的动力学、化学反应器中的浓度分布或机械系统的动力学。具体来说，状态空间模型描述了状态h(t)的演变：

d/dt h(t) = A(t)h(t) + K(t)V(t)，

y(t) = Q(t)h(t) + D(t)V(t)。

在这里，A(t)称为状态矩阵，K(t)是将输入V(t)投影到状态上的输入矩阵，Q(t)是将状态h(t)转换回输出的输出矩阵，D(t)是反馈矩阵。在这里，矩阵Q、K和V的命名预示了它们在查询、键和值中的角色。

在机器学习中，我们处理的是这些方程的离散化版本，序列元素t = 0,1,2,...，而不是连续时间。称Qₜ、Kₜ和Vₜ分别为Q(t)、K(t)和V(t)的离散化对应项。此外，我们选择将A(t)的离散化版本设置为标量aₜ乘以单位矩阵，并且在不失一般性的情况下省略Dₜ。

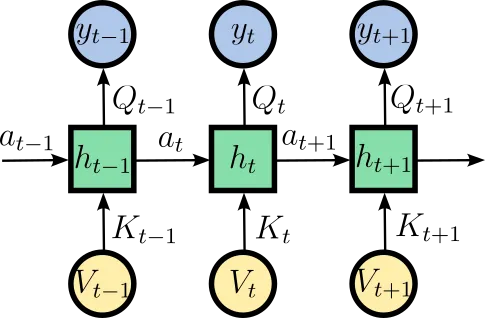
图1

离散形式可以表示为：

hₜ = aₜ hₜ₋₁ + Kₜ Vₜ，

yₜ = Qₜ⊤ hₜ。

注意，这是具有隐藏状态hₜ的循环神经网络（图1）的线性版本。

接下来，定义h₀ = K₀ V₀，并展开递归，我们可以看到yₜ的表达式是一个半可分矩阵：

yₜ = Qₜ⊤aₜ … a₁K₀ V₀ + Qₜ⊤aₜ … a₂K₁ V₁ + Qₜ⊤aₜ … a₃K₂ V₂ + … + Qₜ⊤Kₜ Vₜ

≡ ∑ₛ Mₜₛ Vₛ。

因此，状态空间模型等价于具有特定因果掩码aₜ … a₁的线性注意力。系数aₜ可以被视为可训练的位置编码。重要的是，计算yₜ可以在线性时间而不是二次时间内完成。

使其成为贝叶斯模型

在回顾了基础知识之后，现在考虑一个具有输入x和高斯输出y的单一自注意力块。与往常一样，键K = W(k)x，查询Q = W(q)x，和值V = W(v)x都依赖于输入x。这就是自注意力。我们不再将权重{W(k), W(q), W(v)}视为数字，而是为它们赋予高斯分布。我们对位置编码aₜ也做同样的处理。这有两个关键优势。（i）我们可以在看到数据之前，通过指定我们认为这些权重应该是什么样的——即先验分布——来将领域知识融入到例如权重中。（ii）它允许我们对权重/编码的确切值保持不确定性。

生成模型

现在，我们来指定描述我们认为数据集是如何生成的模型。给定一个包含i = 1...m个输入x的数据集，每个输入x具有t = 0,…,T−1的序列元素，每个元素由R个特征组成。设N为隐藏单元h的维度数。

模型的参数和输出是根据以下统计过程生成的：

在这里，符号x ~ N(μ,Σ)表示：x是从均值为μ、协方差矩阵为Σ的高斯分布中抽取的。换句话说，式（1）表示每个输出y是从隐藏状态h递归生成的，并且每个y都包含一些大小为σ的高斯噪声。此外，键、查询和值权重{W(k), W(q), W(v)}以及位置编码a也是有噪声的实例化，它们位于先验均值p(W)和p(a)附近，并具有预定义的（协）方差。

通过训练模型，我们更新了对权重W和位置编码a的合理值的信念，以及在我们已经看到数据y的情况下，我们对这些信念的坚定程度。

插曲：训练贝叶斯模型

关于训练贝叶斯模型的一点说明。训练机器学习模型的标准方法是找到一组参数Θ = {W(k), W(q), W(v), a}，以优化损失函数——通常是（负）对数似然函数。这与贝叶斯方法不同。在贝叶斯方法中，我们不是为参数Θ找到好的值，而是根据观测值y推断参数的后验分布p(Θ|y)。由于后验分布p(Θ|y)是难以处理的，我们必须对其进行近似。估计p(Θ|y)主要有两种方法。一种方法称为变分推断，它试图优化一个近似p(Θ|y)的替代分布q(Θ)。第二种方法称为马尔可夫链蒙特卡罗（MCMC）模拟。在这里，我们所能做的最好就是从p(Θ|y)中抽取样本Θ。虽然我们不知道如何直接从p(Θ|y)中抽取样本，但我们知道如何达到这个目标。马尔可夫链蒙特卡罗描述了一个随机步骤的过程p(Θₛ|Θₛ₋₁)，当步骤数s足够大时，该过程最终将收敛到p(Θ|y)。

我们还没有指定p(Θₛ|Θₛ₋₁)，即如何采取下一个随机步骤。事实证明，有多个选择p(Θₛ|Θₛ₋₁)可以收敛到后验。在这里，我们将只关注其中一种方法：吉布斯采样。吉布斯采样是一种特别高效的随机步骤方法。一般步骤如下。给定一个由D个参数组成的样本Θₛ₋₁ = [Θₛ₋₁(1), Θₛ₋₁(2), …, Θₛ₋₁(D)]，通过交替抽取每个参数Θₛ(i)（给定之前的值）来采样p(Θₛ|Θₛ₋₁)。即，

• Θₛ(1) ~ p[Θₛ(1)|Θₛ₋₁(2), Θₛ₋₁(3), .., Θₛ₋₁(D), y]，
• Θₛ(2) ~ p[Θₛ(2)|Θₛ(1), Θₛ₋₁(3), .., Θₛ₋₁(D), y]，
• …
• Θₛ(D) ~ p[Θₛ(D)|Θₛ(1), Θₛ(3), .., Θₛ(D-1), y]。

重复此过程，直到Θₛ收敛到后验p(Θ|y)。高效吉布斯采样的一个关键要求是条件分布p[Θₛ(i)|Θₛ(1), Θₛ(2), .., Θₛ(i-1), Θₛ₋₁(i+1), …, Θₛ₋₁(D), y]必须容易从中采样。幸运的是，参数的先验以及似然[式（1）]都是高斯的。这意味着条件分布也必须是高斯的！

使用吉布斯采样进行推断

回到我们的注意力模块。由于参数和输出y都是高斯的，我们可以分析地计算出条件分布。因此，我们可以使用吉布斯采样来得到后验分布。算法如下。

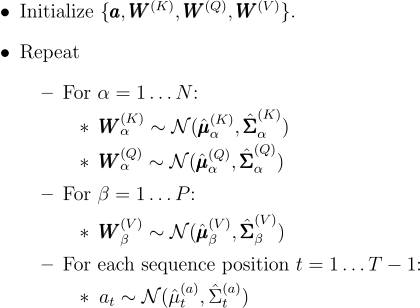
注意到，表示先验均值和协方差的波浪线现已被帽子符号所取代，表示条件均值和协方差。直观地来说，该算法可以被解释为对与回归系数相关的输出进行的一系列交替回归，同时保持其余参数固定。

在JAX代码中，式（2）的内部部分如下所示：

def kernel(key, y, X, state):
  """Take one Gibbs sampling step, updating the model parameters
  Args:
    key: Pseudo random number generator key.
    y: Observed output of the module.
    X: Input to the module.
    state: A tuple with the current model parameters.
  Returns: A new configuration of the (unobserved) model parameters."""
  key_seq = KeySeq(key)
  (ln_a, W_V, W_K, W_Q) = state
  L = jnp.exp(segsum(ln_a))[jnp.newaxis,...]  # Broadcast across batch.
  L = jnp.real(L)  # Discard zero imaginary part.
  # 1) W_K[α] ~ p(W_K[α]|--).
  Q = jnp.einsum('αβ,bsβ->bsα', W_Q, X)
  V = jnp.einsum('pi,bsi->bsp', W_V, X)
  W_K = sample_weights_keys(next(key_seq), W_K, Q, V, L, X, y)
  # 2) W_Q[α] ~ p(W_Q[α]|--).
  K = jnp.einsum('nk,bsk->bsn', W_K, X)
  W_Q = sample_weights_queries(next(key_seq), W_Q, K, V, L, X, y)
  # 3) W_V[β] ~ p(W_V[β]|--).
  Q = jnp.einsum('αβ,bsβ->bsα', W_Q, X)
  W_V = sample_weights_values(next(key_seq), W_V, K, Q, L, X, y)
  # 4) a[t] ~ p(a[t]|--).
  V = jnp.einsum('pi,bsi->bsp', W_V, X)
  ln_a = sample_positional_encodings(next(key_seq), ln_a, K, V, Q, X, y)
  state = (ln_a, W_V, W_K, W_Q)
  return state

在这里，segsum构建了因果掩码L（下文描述），而KeySeq是一个用于伪随机数生成器记账的辅助类。

接下来，我们将逐一介绍各个采样函数。

采样位置编码aₜ

为了对位置编码系数aₜ进行吉布斯采样，我们将预测分解为与aₜ成比例和与aₜ无关的项：

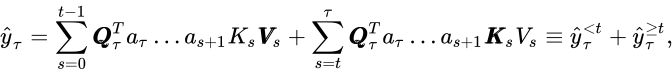
（暂时）我们省略了训练样本索引i和特征索引p。注意到只有在? ≥ t的情况下，y的较小值预测中才包含aₜ项。这是生成模型[式（1）]的直接结果，其中aₜ项进入hₜ = aₜ hₜ₋₁ + Kₜ Vₜ，因此只影响yₜ及之后的输出。通过乘以和除以aₜ，我们可以看出这是一个带截距y的较大值的回归。经过一些计算后，式（2）中的均值和方差结果为：

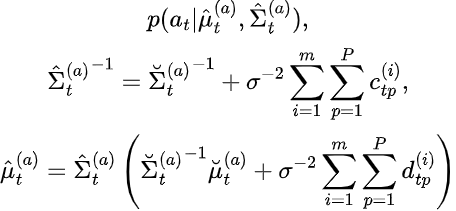
其中，我们将c和d项定义为：

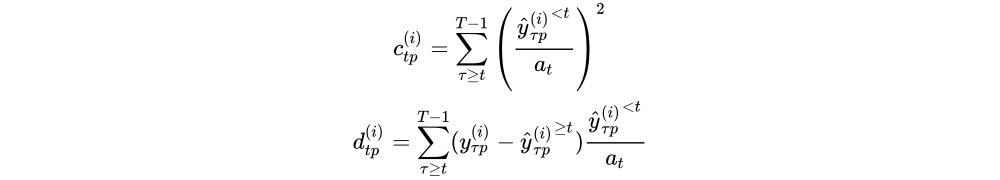
这些可以被解释为精度和相关性的一种度量。

在代码中，我们将状态aₜ的对数存储为复数，以跟踪负号。此外，我们构建了因果掩码矩阵L，其中下三角元素设置为Lₜₛ = aₜ … aₛ₊₁，对角线元素为1。

def sample_positional_encodings(key, ln_a, K, V, Q, X, y):
  key_seq = KeySeq(key)
  G = jnp.einsum('btn,bsn->bts', Q, K)
  for t in range(1, T):
    L = jnp.exp(segsum(ln_a))[None,...]  # (B,T,S)
    L = jnp.real(L) # Discard zero imaginary part.
    M = jnp.einsum('bts,bts->bts', G, L)
    # Compute y<.
    y_pred_cumul = jnp.cumsum(
        M[..., jnp.newaxis] * V[:,jnp.newaxis,...], axis=-2,
    )  # (B,T,S,P)
    y_pred = y_pred_cumul.diagonal(axis1=-3, axis2=-2)  # (B,P,T)
    y_pred = rearrange(y_pred, 'b p t -> b t p')
    mask = jnp.triu(jnp.ones([T, T], dtype=bool))  # (T,S)
    mask = mask[jnp.newaxis, ..., jnp.newaxis]  # (B,T,S,P)
    y_pred_lt = jnp.where(mask, 0, y_pred_cumul)
    # Insert column with zeros at index 0.
    y_pred_lt = jnp.pad(y_pred_lt, ((0, 0), (0, 0), (1, 0), (0, 0)))
    y_pred_lt = y_pred_lt[..., :-1,:]  # (B,T,S,P)
    # Interpret as a regression with regression coefficient a:
    # y-y≥ = a * (y< / a),
    # where we move all terms not containing `a` into the output.
    y_pred_lt_t = y_pred_lt[...,t,:]
    y_pred_ge_t = y_pred - y_pred_lt_t  # y≥.
    is_geg_t = (jnp.arange(T) >= t).astype(int)[None, :, None]  # (B,T,P)
    outputs = (y - y_pred_ge_t) * is_geg_t  # tau >= t
    outputs = rearrange(outputs, 'b t p->(b t p)')
    a_t = jnp.real(jnp.exp(ln_a[t]))
    inputs = y_pred_lt_t * is_geg_t / a_t  # (B,T,P)
    inputs = rearrange(inputs, 'b t p->(b t p)')
    μ_a_posterior, σ_a_posterior = scalar_gaussian_posterior(
        outputs, inputs, μ_a_prior[t], Λ_a_prior[t],
    )
    a_t = random.normal(next(key_seq)) * σ_a_posterior + μ_a_posterior
    ln_a = ln_a.at[t].set(jnp.log(a_t.astype(complex)))
  return ln_a

在这里，scalar_gaussian_posterior函数计算单变量高斯回归的均值和方差。

采样键权重W(k)

为了采样键权重W(k)，注意到我们可以将预测输出表示为W(k)和矩阵Γ之间的点积。利用高斯分布的共轭关系，条件均值和协方差矩阵为：

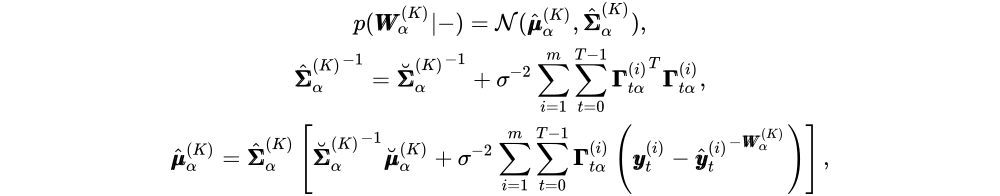
其中我们定义了，

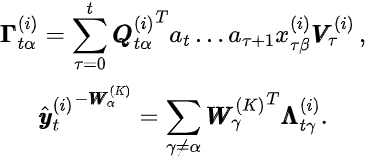
将这些方程解释为线性回归时，可以将Γ视为协变量，将不包含W(k)的第α=1…N行的预测视为偏移量，将y视为输出。如式（2）所示，每一行是单独采样的。在代码中，采样步骤如下：

def sample_weights_keys(key, W_K, Q, V, L, X, y):
  key_seq = KeySeq(key)
  Γ = jnp.einsum('btα,bts,bsβ,bsp->btpαβ', Q, L, X, V)
  for α in range(n_components):
    y_pred = jnp.einsum('αβ,btpαβ->btp', W_K, Γ)
    y_pred_α = jnp.einsum('β,btpβ->btp', W_K[α], Γ[:,:,:,α])
    y_residual = y - (y_pred - y_pred_α)
    y_residual = rearrange(y_residual, 'b t p->(b t p)')
    λ = rearrange(Γ[:,:,:,α], 'b t p β->(b t p) β')
    μ, Σ = gaussian_posterior(
        y_residual, μ_prior=μ_k_prior[α], Λ_prior=Λ_k_prior[α], X=λ,
    )
    w_α = random.multivariate_normal(next(key_seq), μ, Σ)
    W_K = W_K.at[α].set(w_α)
  return W_K

其中，gaussian_posterior函数计算多元贝叶斯回归的均值和协方差矩阵。

采样查询权重W(q)

接下来，对应查询的权重的采样几乎完全相同。将问题视为具有协变量的回归问题，

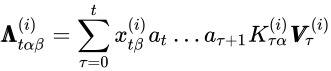
查询权重W(q)可以使用条件分布进行采样。

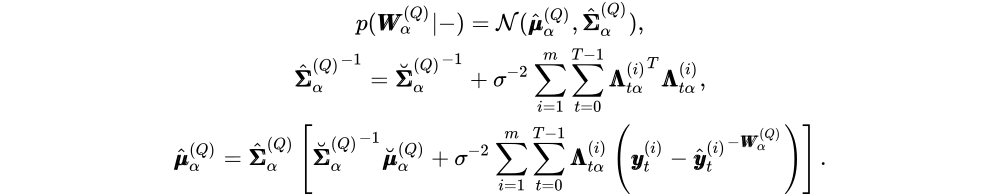
不出所料，代码与sample_weights_keys相似，只是对协变量和截距做了细微修改：

def sample_weights_queries(key, W_Q, K, V, L, X, y):
  key_seq = KeySeq(key)
  Λ = jnp.einsum('btβ,bts,bsα,bsp->btpαβ', X, L, K, V)
  for α in range(n_components):
    y_pred = jnp.einsum('αβ,btpαβ->btp', W_Q, Λ)
    y_pred_α = jnp.einsum('β,btpβ->btp', W_Q[α], Λ[:,:,:,α])
    y_residual = y - (y_pred - y_pred_α)
    y_residual = rearrange(y_residual, 'b t p->(b t p)')
    λ = rearrange(Λ[:,:,:,α], 'b t p β->(b t p) β')
    μ, Σ = gaussian_posterior(
        y_residual, μ_prior=μ_k_prior[α], Λ_prior=Λ_k_prior[α], X=λ,
    )
    w_α = random.multivariate_normal(next(key_seq), μ, Σ)
    W_Q = W_Q.at[α].set(w_α)
  return W_Q

采样值权重W(v)

对应于W(v)回归的协变量为：

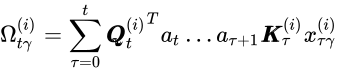
与键和查询的条件分布不同，该回归不再包含截距项。条件分布如下：

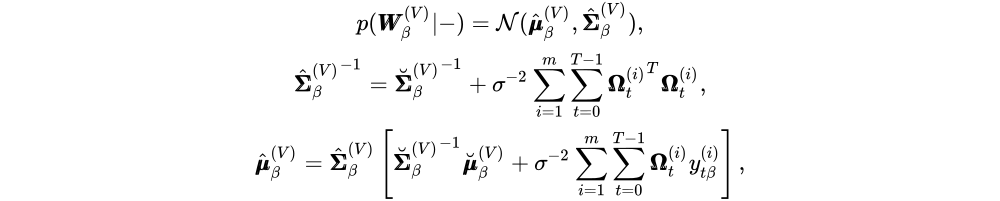
每一行，β = 1…P，单独采样，并对应于一个单独的输出维度。

def sample_weights_values(key, W_V, K, Q, L, X, y):
  key_seq = KeySeq(key)
  Ω = jnp.einsum('btn,bts,bsn,bsβ->btβ', Q, L, K, X)
  Ω = rearrange(Ω, 'b t β->(b t) β')
  y_pred = jnp.einsum('βγ,iγ->iβ', W_V, Ω)
  y_flat = rearrange(y, 'b t α->(b t) α')
  for β in range(p_features):
    y_β = y_flat[:,β]
    μ, Σ = gaussian_posterior(
        y_β, μ_prior=μ_v_prior[β], Λ_prior=Λ_v_prior[β], X=Ω,
    )
    w_β = random.multivariate_normal(next(key_seq), μ, Σ)
    W_V = W_V.at[β].set(w_β)
  return W_V

整合起来

现在我们已经有了所有的单独采样步骤，我们可以训练模型了。如式（2）所示，在初始化参数后，你反复调用之前定义的kernel函数，直到收敛到后验分布。吉布斯采样器有时会陷入局部最优。因此，总是要检查似然性，并比较不同的起点，以查看模型是否正确识别了后验模式。最后，在收敛到后验分布后，你只需收集状态样本以估计后验分布。

如果成功，模型训练可能如下所示：

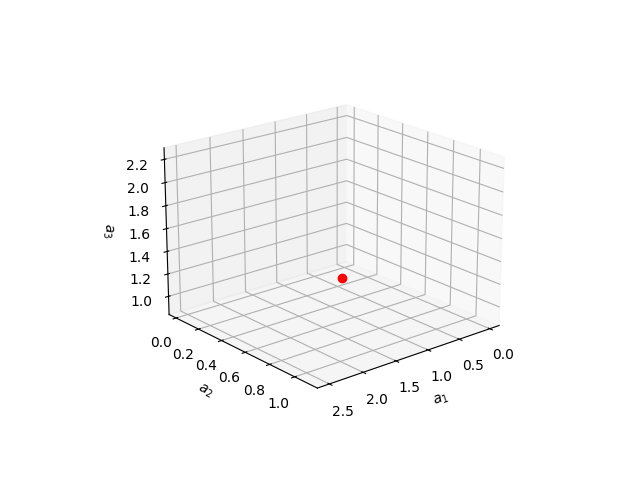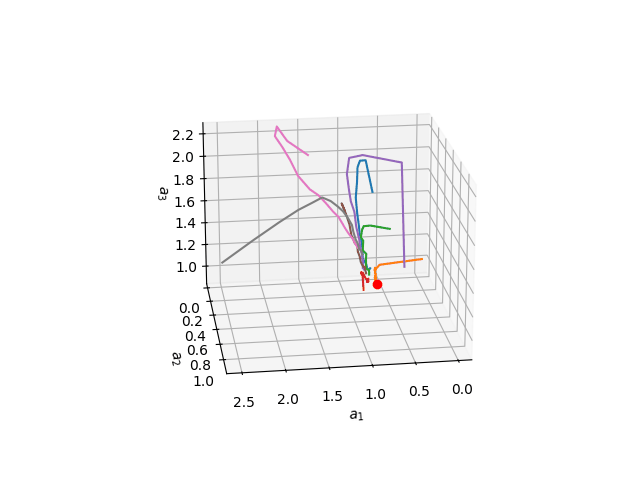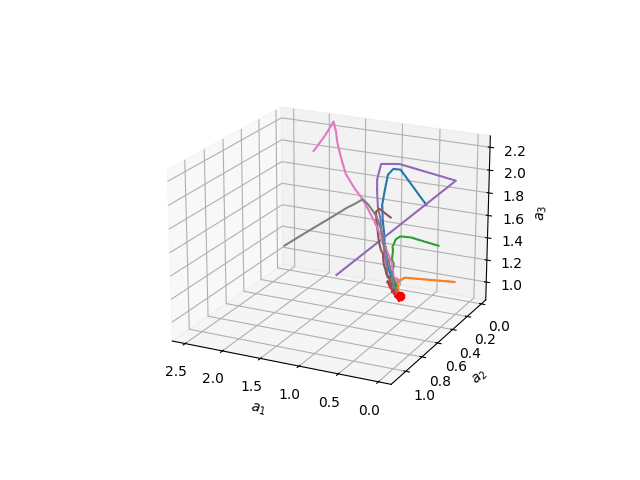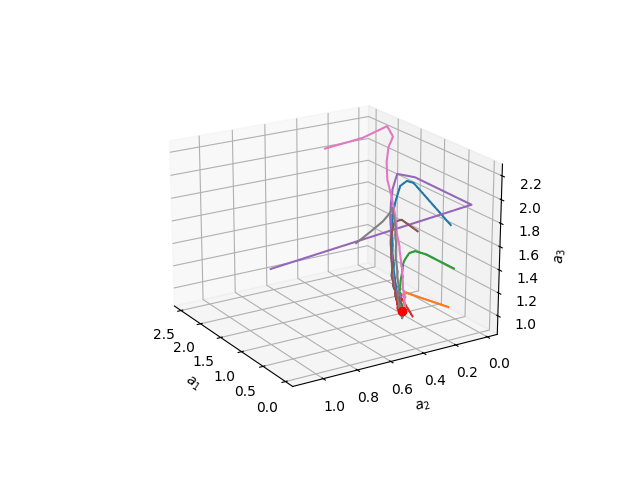
干得好！? 你已经成功从头开始实现了贝叶斯注意力机制！

结论

我们利用将注意力机制与状态空间模型和半可分矩阵联系起来，提出了自注意力的贝叶斯对应物，以建模和预测小规模的序列集。我们看到了如何对位置编码以及与键、查询和值相关的参数进行不确定性感知估计。当你的训练集很小时（例如，只有十几个例子），贝叶斯注意力特别强大。使用先验，你可以在数据很少时，在启发式方法/领域知识之间进行插值，而在数据很多时，进行完全数据驱动的预测。然而，基于马尔可夫链蒙特卡罗的方法在扩展到大型数据集和许多特征时仍然具有挑战性。