理解预测中的不确定性与预测本身同样重要。点预测告诉我们对未来值的最佳估计，而置信区间则帮助我们了解可能结果的范围。

当我们对未来进行预测时，随着预测时间的延长，不确定性也会增加。这种不断增加的不确定性源于多个方面：模型不确定性、参数不确定性以及我们试图预测的系统中固有的随机性。置信区间帮助我们量化和传达这种不确定性。

计算预测置信区间

让我们以ARIMA模型为例开始实践，ARIMA模型提供了内置的置信区间计算功能。

我使用的是ERCOT的电力需求数据。该数据每15分钟报告一次。为了便于分析，我将数据重新采样为每小时一次。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from sklearn.preprocessing import StandardScaler
from pmdarima import auto_arima
import warnings
warnings.filterwarnings("ignore")
# Load and preprocess data
def load_and_preprocess_data(url):
    df = pd.read_csv(url)
    df['date'] = pd.to_datetime(df['date'])
    df.set_index('date', inplace=True)
    df = df.resample('h').mean().asfreq('h')
    df['values'] = df['values'].interpolate()
    scaler = StandardScaler()
    df['scaled_values'] = scaler.fit_transform(df[['values']])
    return df, scaler
# Forecast with ARIMA
def forecast_with_confidence(data, order, steps=48, confidence=0.95):
    model = ARIMA(data, order=order)
    fitted_model = model.fit()
    
    forecast_result = fitted_model.get_forecast(steps=steps)
    forecasts = forecast_result.predicted_mean
    conf_int = forecast_result.conf_int(alpha=1 - confidence)
    return forecasts, conf_int.iloc[:, 0], conf_int.iloc[:, 1]
# Plot function
def plot_forecast_with_ci(historical_data, test_data, forecasts, lower_ci, upper_ci, title="Forecast with Confidence Intervals"):
    plt.figure(figsize=(12, 6))
    plt.plot(historical_data.index, historical_data.values, label='Historical Data', color='blue')
    plt.plot(test_data.index, test_data, label='Actual Test Data', color='green')
    
    forecast_index = test_data.index
    plt.plot(forecast_index, forecasts, 'r-', label='Forecast')
    plt.fill_between(forecast_index, lower_ci, upper_ci, color='r', alpha=0.2, label='95% CI')
    plt.axvline(x=test_data.index[0], color='black', linestyle='--', label="Test Data Start")
    plt.title(title)
    plt.xlabel('Date')
    plt.ylabel('Value')
    plt.legend()
    plt.xticks(rotation=45)
    plt.tight_layout()
    plt.savefig(f'{title}.png')
    plt.show()
# Main workflow
url = "https://raw.githubusercontent.com/kylejones200/time_series/refs/heads/main/ercot_load_data.csv"
df, scaler = load_and_preprocess_data(url)
train_data = df['scaled_values'].iloc[:-48]
test_data = df['scaled_values'].iloc[-48:]
# Find best ARIMA order
auto_model = auto_arima(train_data, seasonal=False, trace=True, suppress_warnings=True, stepwise=True)
best_order = auto_model.order
print(f"Using ARIMA order: {best_order}")
# ARIMA forecast with confidence intervals
forecasts, lower_ci, upper_ci = forecast_with_confidence(train_data, best_order, steps=48)
# Bootstrapped confidence intervals
boot_forecasts, boot_lower_ci, boot_upper_ci = bootstrap_forecast_ci(best_order, train_data, steps=48, n_bootstraps=50)
def inverse_transform_and_flatten(scaler, data):
    return scaler.inverse_transform(np.array(data).reshape(-1, 1)).flatten()

forecasts, lower_ci, upper_ci = map(lambda x: inverse_transform_and_flatten(scaler, x), [forecasts, lower_ci, upper_ci])
boot_forecasts, boot_lower_ci, boot_upper_ci = map(lambda x: inverse_transform_and_flatten(scaler, x), [boot_forecasts, boot_lower_ci, boot_upper_ci])
test_data_original = inverse_transform_and_flatten(scaler, test_data)

test_data_original_series = pd.Series(test_data_original, index=test_data.index)
# Plot results
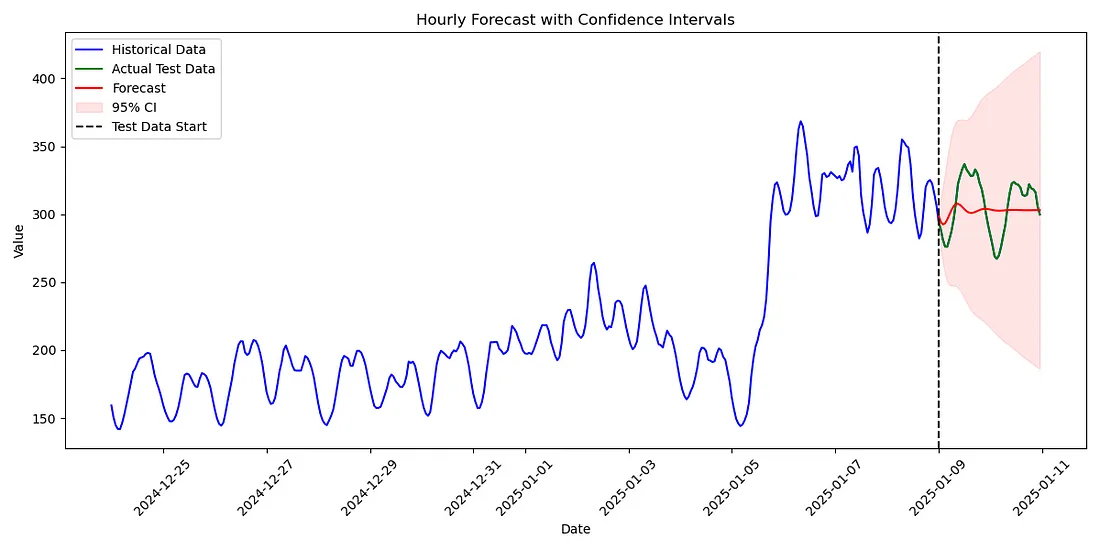
plot_forecast_with_ci(df['values'], test_data_original_series, forecasts, lower_ci, upper_ci, title="ARIMA Forecast with Confidence Intervals")
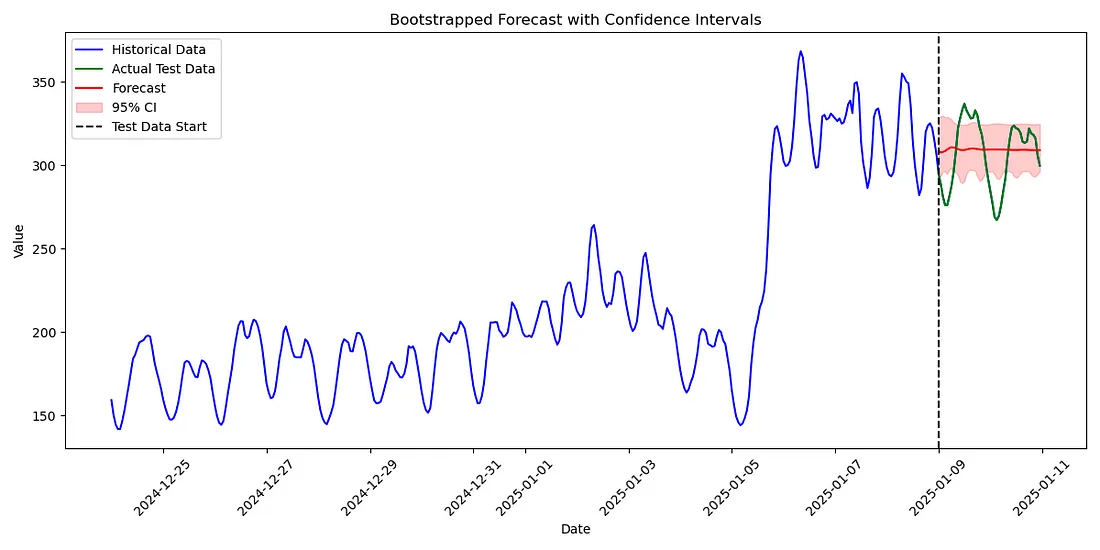
plot_forecast_with_ci(df['values'], test_data_original_series, boot_forecasts, boot_lower_ci, boot_upper_ci, title="Bootstrapped Forecast with Confidence Intervals")

对于不提供内置置信区间的模型，我们可以使用自助法（bootstrap methods）来估计预测区间。

# Bootstrap-based forecast confidence intervals
def bootstrap_forecast_ci(model_order, data, steps=48, n_bootstraps=100, confidence=0.95):
    forecasts = []
    
    for i in range(n_bootstraps):
        try:
            bootstrap_sample = data.sample(n=len(data), replace=True).sort_index()
            model = ARIMA(bootstrap_sample, order=model_order)
            fitted_model = model.fit()
            forecasts.append(fitted_model.forecast(steps=steps).values)
        except Exception as e:
            print(f"Bootstrap iteration {i} failed: {e}")
    if not forecasts:
        raise RuntimeError("All bootstrap iterations failed.")
    forecasts = np.array(forecasts)
    lower_ci = np.percentile(forecasts, (1 - confidence) / 2 * 100, axis=0)
    upper_ci = np.percentile(forecasts, (1 + confidence) / 2 * 100, axis=0)
    mean_forecast = np.mean(forecasts, axis=0)
    return mean_forecast, lower_ci, upper_ci
# Bootstrapped confidence intervals
boot_forecasts, boot_lower_ci, boot_upper_ci = bootstrap_forecast_ci(best_order, train_data, steps=48, n_bootstraps=50)
boot_forecasts, boot_lower_ci, boot_upper_ci = map(lambda x: inverse_transform_and_flatten(scaler, x), [boot_forecasts, boot_lower_ci, boot_upper_ci])
# Plot results
plot_forecast_with_ci(df['values'], test_data_original_series, boot_forecasts, boot_lower_ci, boot_upper_ci, title="Bootstrapped Forecast with Confidence Intervals")

解释置信界限

置信区间需要谨慎解释。95%的置信区间并不意味着我们有95%的把握认为真实值会落在这个区间内。相反，它的意思是，如果我们多次重复这个过程，大约95%的区间会包含真实值。

使用置信区间的最佳实践

在处理置信区间时，重要的是要考虑更广泛的背景。区间的宽度具有意义——宽区间表明不确定性更大，而窄区间则表明精确度更高。然而，这种解释取决于特定的数据集和应用场景。

置信区间依赖于基本假设，如数据的分布或所选的统计模型。清晰地传达这些假设有助于他人理解你结果的可靠性。

有效的可视化可以增强理解，尤其是在向不同受众展示时。无论是使用图表中的阴影区域、误差条还是其他图形技术，目标都是使不确定性直观且易于理解。

考虑多个置信水平可以提供更细致的观点。虽然95%的区间很常见，但探索80%的区间可能会突出显示否则会被掩盖的模式或趋势。

最后，置信区间不应该是静态的——它们需要持续验证。定期用样本外数据测试区间，确保它们保持良好校准，从而增强其在实际应用中的可靠性。