简介

关于

这项工作介绍了Autoformer，一种专门为长期时间序列预测设计的基于Transformer的架构。通过将序列分解框架与新颖的自动相关机制相结合，Autoformer引入了一种强大的方法来更好地捕捉时间模式。这种结合使模型能够逐步从复杂序列中提取趋势和季节性成分，从而最终降低计算成本并提高预测准确性。

背景

随着Transformer模型的日益流行，其在时间序列预测中的应用受到了广泛关注。特别是，Transformer在解决传统模型（如RNN和LSTM）难以应对的长期预测挑战方面表现出了潜力。

然而，使用标准的Transformer架构来处理时间序列数据存在局限性。作者指出，直接建模长距离时间依赖性通常效果不佳，且现有的自注意力机制计算开销较大。为了解决这些问题，Autoformer用序列式自动相关机制取代了传统的自注意力机制，使模型能够更好地识别并利用长期的重复模式。

方法

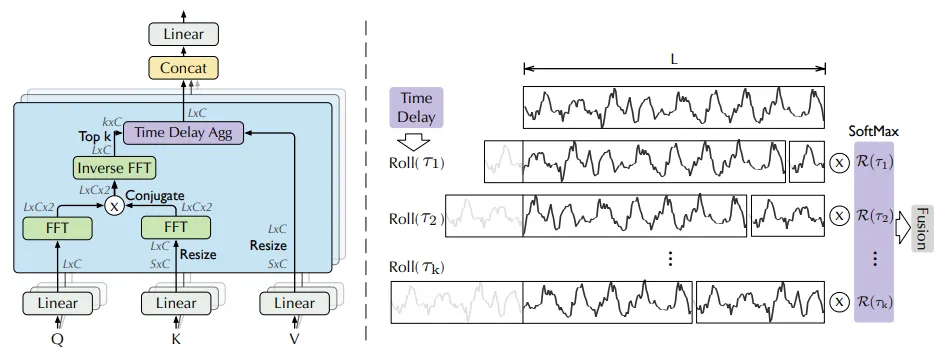
图1

这项工作旨在解决长期预测问题，即在给定过去长度为I的序列的情况下预测未来最有可能的长度为O的序列。这个问题定义被称为输入-I-预测-O。为了解决与这个大输出长度O相关的挑战，作者提出了以下两种新结构：分解架构和自动相关机制。

分解架构

本文提出的分解方法遵循现有时间序列分解的概念。具体而言，这种方法考虑了趋势-周期部分和季节性部分，分别相当于序列的长期进展和季节性。作者在一个序列分解块中实现了这个概念。首先，以移动平均的方式来平滑掉周期性波动，并突出长期趋势。给定长度为L的输入序列X ∈ ℝᴸᕽᵈ，具体的移动平均方法如下：

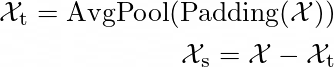
请注意，?ₛ 和 ?ₜ 分别表示提取出的季节性部分和趋势-周期性部分。通过填充操作进行的平均池化操作可以保持序列长度不变。这个简单的过程在图1中称为SeriesDecomp块。

Autoformer编码器部分的时间序列输入为过去I个时间步长 ?(en) ∈ ℝᴵᕽᵈ。Autoformer解码器部分有两个输入：季节性部分 ?(des) 和趋势-周期性部分 ?(det)。这两个特征通过编码器中给定的分解序列 ?(ens) 和 ?(ent) 聚合在一起。

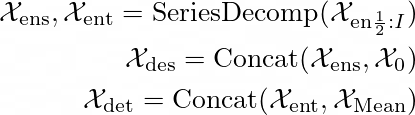
这里，符号 ?₀ 和 ?(Mean) 分别指代零填充的占位符和 ?(en) 的均值。

与经典的 Transformer 模型类似，Autoformer 的编码器块也由 N 个编码器层组成。第 l 层编码器层的操作可以表示为 ?ˡ(en) = Encoder(?ˡᐨ¹(en))。详细过程如下所示。

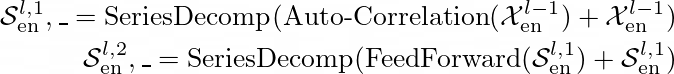
结果 ?ˡ`ⁱ(en), i ∈ {1, 2} 分别表示经过第 l 层中的第 i 个序列分解块处理后的季节性分量。请注意，此部分未使用相应的趋势输出。自动相关操作将在以下部分中解释。

解码器部分包括累积结构和堆叠的自动相关机制。每个部分代表两个时间序列分解后的特征。解码器在操作过程中从中间隐藏变量中提取潜在趋势。这使得整个网络能够逐步优化趋势预测，并消除基于周期的依赖性发现中的干扰信息。本文中的解码器块具有 M 个解码器层。第 l 层解码器层的操作可以表示为 ?ˡ(de) = Decoder(?ˡ(de), ?ᴺ(en))。整个过程如下。

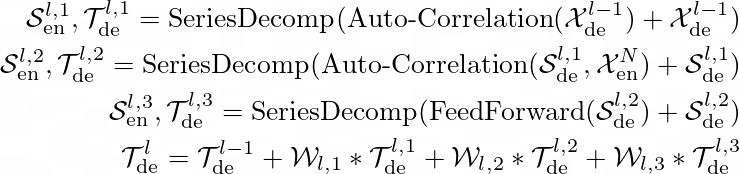
这里，?ˡ(de) 等于 ?ˡ`³(en)。趋势部分 ?ˡ(de) 通过权重参数 ?ˡ 进行额外处理。最终预测结果是这两个优化后的分解分量的总和。

自动相关机制

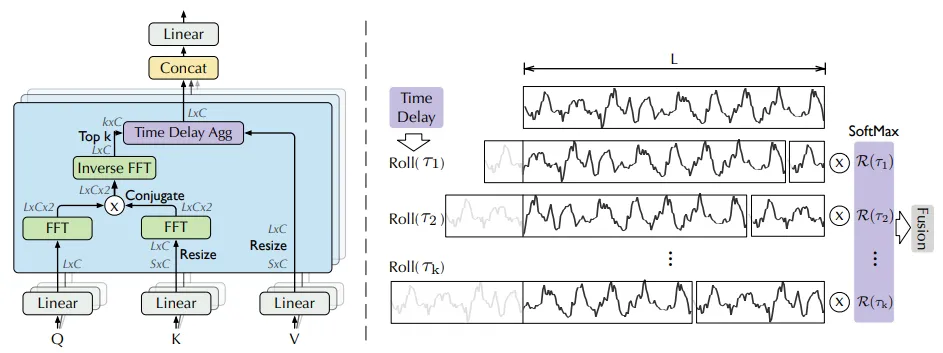
图2

本文中的自动相关方法遵循传统方法。请注意，此部分的时间序列元素通过快速傅里叶变换 (FFT) 进行预处理，返回离散特征 ?ₜ。自相关 ℛₓₓ(?) 是通过以下方程进行的。

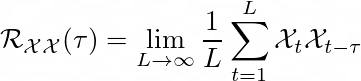
这表示 ?ₜ 与其 ? 滞后序列 ?(t-?) 之间的时间延迟相似性。? 代表估计周期长度的未归一化置信度。作者选择了最可能的 k 个周期长度 ?₁, ···, ?ₖ。

图1中的时间延迟聚合方法表示基于选择的时间延迟 ?₁, ···, ?ₖ 滚动序列，并最终通过 SoftMax 归一化的置信度结合来自自动相关过程的最终特征。

对于单头情况和长度为 L 的时间序列 ?，对应的查询 (Query) ?、键 (Key) ? 和值 (Value) ? 是通过传统投影器收集的。具体过程参考以下方程。

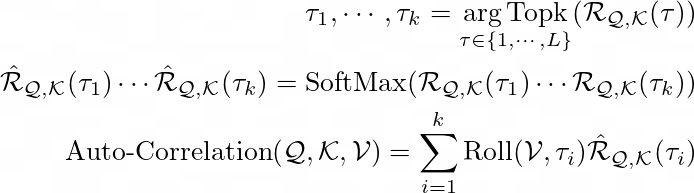
其中，Topk 用于获取前 k 个自相关的参数，并令 k = ⌊ c ⨉ log L ⌋，c 是一个超参数。ℛ 是序列 ? 和 ? 之间的自相关。Roll(?, ?) 表示对 ? 进行时间延迟为 ? 的操作，在此过程中，超出首位置的元素会重新引入到最后位置。多头情况如下所示，其中第 i 个头的查询 (Query)、键 (Key) 和值 (Value) 分别为 ?ᵢ, ?ᵢ, ?ᵢ。

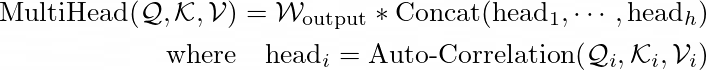
这些注意力机制的复杂度是 ?(L log L)。

作者基于 Wiener-Khinchin 定理进行了快速傅里叶变换 (FFT)。

这里，? ∈ {1, ···, L}，ℱ 是 FFT 而 ℱᐨ¹ 是逆 FFT。* 表示共轭操作。虽然经典的自注意机制由于逐点乘法需要大量的计算成本，但提出的方法实现了更少的资源需求。整个过程如图2所示。

实验

数据集

作者使用了6个真实世界基准，其中包括5个公开的时间序列数据集。

• ETT
• Electricity
• Exchange
• Traffic
• Weather
• ILI

对于 ETT 数据集，训练-验证-测试的比例是6:2:2，剩余数据集的比例是7:1:2。

模型设置

• 损失：L2
• 优化器：Adam
• 学习率：0.0001
• 批量大小：32
• 轮数：10以内
• 实验重复次数：3

对比模型

作者引用了10种现存的时间序列预测网络作为对比模型。

多变量情况

Informer, Reformer, LogTrans, LSTNet, LSTM, TCN

单变量情况

N-BEATS, DeepAR, Prophet, ARIMA

评估指标

使用了常用指标均方误差（MSE）和平均绝对误差（MAE）。

结果

主要结果

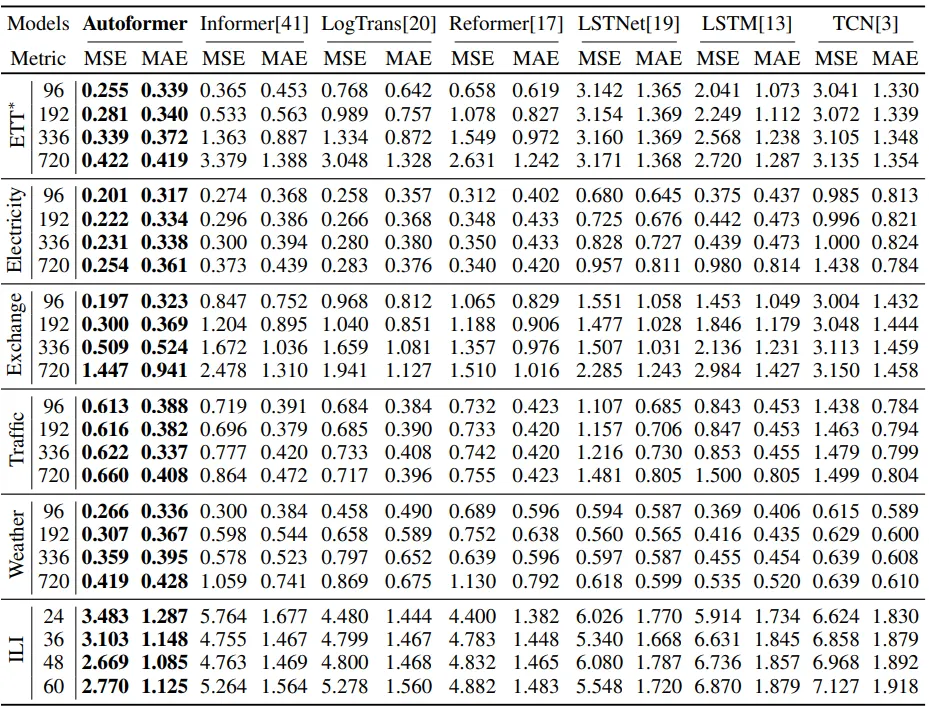
图3

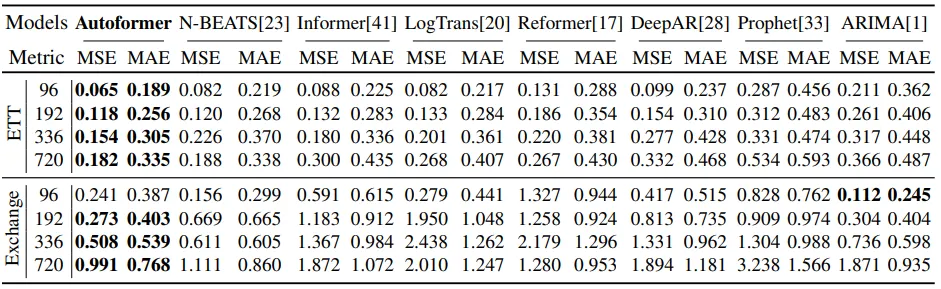
图4

首先进行了多变量实验。作者设计了具有不同预测距离的实验。相应结果显示在图3中。在ETT数据集上的实验表明，该方法优于所有比较的模型。特别是，随着序列预测任务长度的增加，预测性能的差异变得更大。

单变量测试的结果也显示在图4中。这些结果在除ARIMA单例外的所有结果中都表现优异。

消融研究

作者设计了消融研究以探索所提出的两种方法的效用。

分解架构

图5

作者报告了将分解方法插入到其他模型和原始网络中的结果。比较结果如图5所示。这些结果表明，所提出的分解方法无论在何种架构中都能产生优越的预测效果。

自动相关

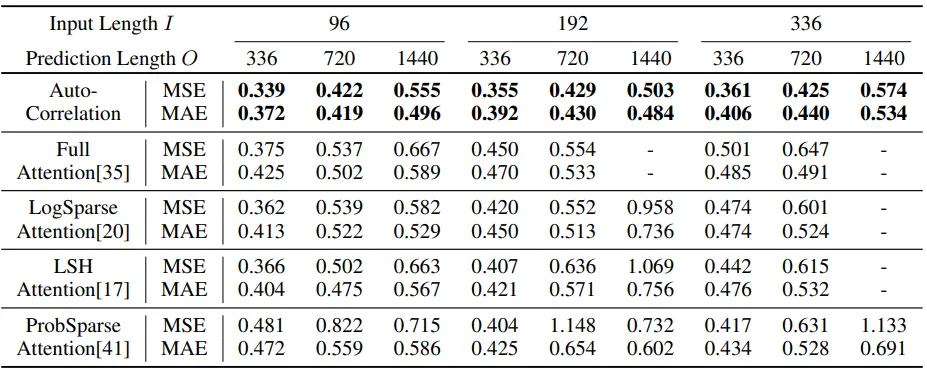
图6

作者进行了一个性能比较实验，将所提出的自动相关方法与现有的注意力机制进行了比较。结果如图6所示。现有的注意力方法在预测长度较长时效果不佳，而带有自动相关的网络则返回了稳健的结果。

模型分析

时间序列分解

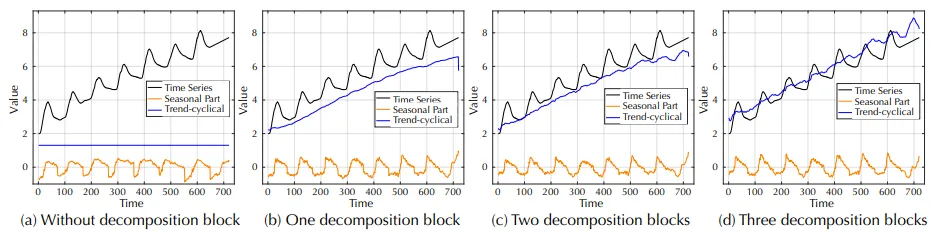
图7

图7展示了从分解块中可视化的特征。通过添加序列分解块，所提出的Autoformer可以逐步聚合和优化序列中的趋势-周期性部分。

依赖关系学习

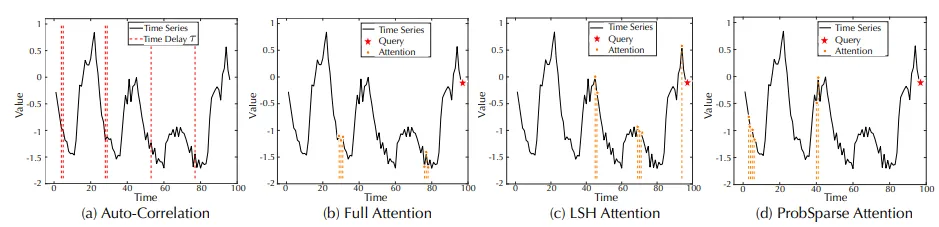
图8

如图8 (a) 所示，相较于经典注意力技术，自动相关方法能够充分利用所有相似的子序列，不会有遗漏或错误。

复杂季节性建模

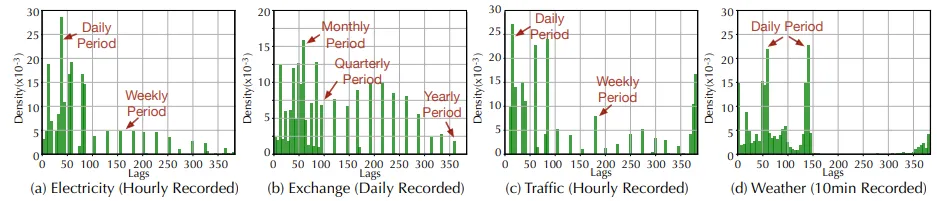
图9

图9的延迟结果表明，Autoformer模型能够从深度表示中捕捉现实世界序列的复杂季节性。此外，该网络提供了一个可供人类解读的预测。

效率分析

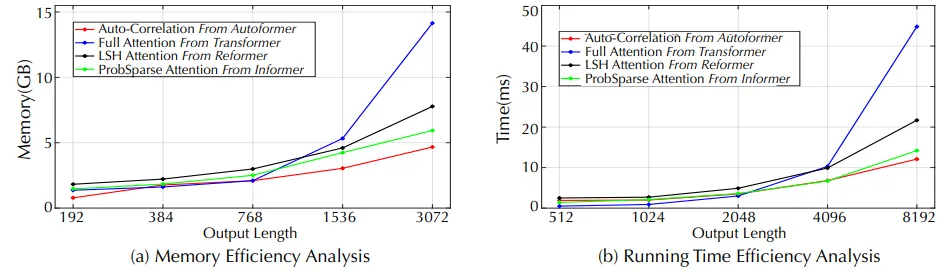
图10

如图10所示，与其他传统Transformer模型相比，所提出的Autoformer显著降低了内存复杂度。

结论

本文介绍的Autoformer在时间序列预测领域，尤其是长期预测方面迈出了重要一步。通过将序列分解与新颖的自动相关机制相结合，该模型有效地降低了计算开销，同时在一系列复杂数据集中提供了最先进的预测性能。其架构不仅解决了传统Transformer在时间序列任务中的核心限制，还为可扩展、高效的预测模型开辟了新可能。