柯尔莫哥洛夫 - 阿诺德网络（KAN）是基于柯尔莫哥洛夫 - 阿诺德表示定理的神经网络架构。该定理指出，任何多元连续函数都可以表示为连续一元函数的和以及一个辅助函数。这使得柯尔莫哥洛夫 - 阿诺德网络具有很强的表达能力，非常适合对时间序列数据中的复杂非线性关系进行建模。

KAN 可以表示变量之间复杂的非线性依赖关系。它们有助于降低维度。它们可以逼近任何连续函数，使其能够灵活地应用于各种时间序列应用。

在这个项目中，我们将KAN应用于一项基于来自FRED的美国零售销售数据的实际时间序列预测任务。我们将其与经典预测的主力方法——自回归整合移动平均模型（ARIMA）进行了直接对比，结果令人惊讶。

我们使用来自美联储经济数据 (FRED) API 的月度美国零售销售（不包括食品服务）指数 (RSXFS)。该数据集跨越十多年，反映了长期经济增长、新冠疫情等短期冲击以及节假日周期的季节性变化。

KAN

KAN是基于一元分解的通用逼近器。我们的简单模型使用过去12个月的零售销售数据，训练了超过100个周期。 

class KolmogorovArnoldNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super().__init__()
        self.decomposition = nn.Linear(input_dim, hidden_dim)
        self.aggregation = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
        h = torch.tanh(self.decomposition(x))
        return self.aggregation(h)

我们采用了滚动窗口来构建输入序列，并使用80%的数据对模型进行训练，剩余20%的数据则用于测试。

ARIMA是时间序列预测领域的黄金标准。 

from statsmodels.tsa.arima.model import ARIMA
model_arima = ARIMA(train_values, order=(5, 1, 0)).fit()

它对自回归、差分和移动平均进行建模，但无法直接处理非线性关系。

评估

我们使用测试集上的均方根误差（RMSE）来比较各个模型。

KAN：6745.67

ARIMA：18121.76

KAN的表现优于ARIMA。它的均方根误差比ARIMA低60%。

这证实了KAN在捕捉传统模型可能会忽略的非线性动态方面的优势。尽管KAN结构简单，但它的泛化能力很强，能够跟踪短期变化而不会出现过拟合的情况。

以下是直观的视觉呈现：

预测值与实际值对比（测试集） 

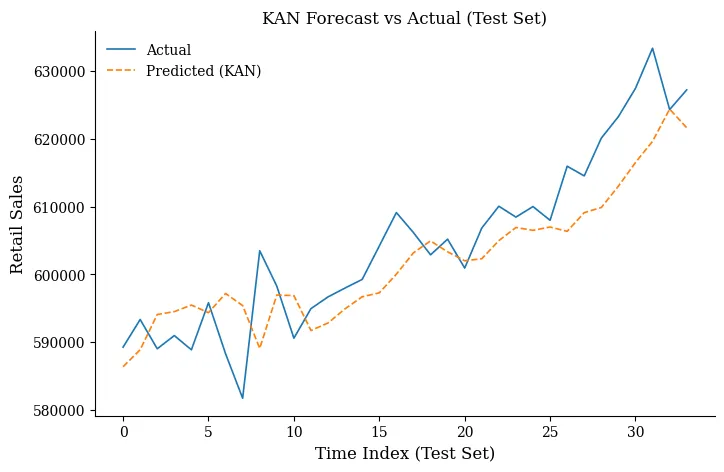
未来两年的预测

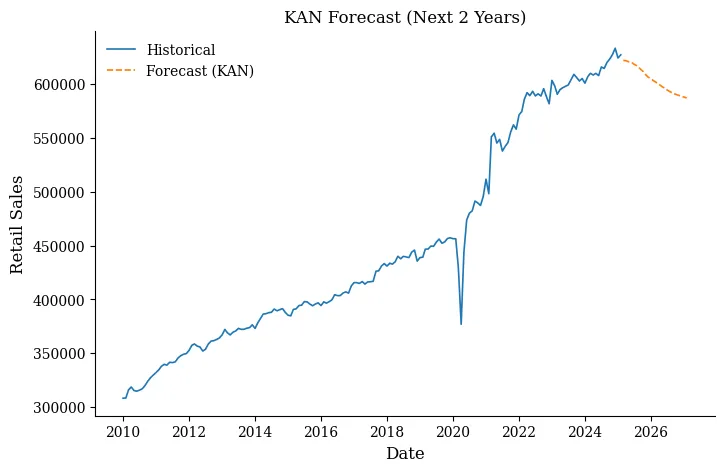
为什么KAN会胜出？

tanh激活函数使KAN能够构建出高度非线性的曲线。即使是浅层网络，只要问题存在ARIMA无法建模的复杂性，KAN就能够表现得更出色。12个月的滚动输入为模型提供了时间背景信息。

要点总结

在PyTorch中构建KAN很容易。只需几行代码，你就能在真实世界的数据上取得最先进的成果。

自回归整合移动平均模型（ARIMA）仍然有用——但在存在非线性增长、冲击或非平稳行为的领域中，深度学习方法能够大放异彩。

零售销售数据集（RSXFS）是一个很有用的基准——它具有可解释性、真实性，并且结构丰富。

完整代码 

import pandas as pd
import numpy as np
import datetime
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
import torch
import torch.nn as nn
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt
# Fetch FRED data
start = datetime.datetime(2010, 1, 1)
end = datetime.datetime.today()
df = web.DataReader("RSXFS", "fred", start, end).dropna().reset_index()
df.columns = ["date", "value"]
df['date'] = pd.to_datetime(df['date'])
# Normalize for KAN
scaler = MinMaxScaler()
scaled_values = scaler.fit_transform(df[["value"]].values)
# Create lagged input-output for KAN
window_size = 12
X, y = [], []
for i in range(len(scaled_values) - window_size):
    X.append(scaled_values[i:i + window_size].flatten())
    y.append(scaled_values[i + window_size][0])
X, y = np.array(X), np.array(y).reshape(-1, 1)
# Chronological train-test split
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
# Convert to tensors
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32)
# Define KAN model
class KolmogorovArnoldNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super().__init__()
        self.decomposition = nn.Linear(input_dim, hidden_dim)
        self.aggregation = nn.Linear(hidden_dim, output_dim)
    def forward(self, x):
        h = torch.tanh(self.decomposition(x))
        return self.aggregation(h)
# Train KAN
input_dim = window_size
model = KolmogorovArnoldNetwork(input_dim, 10, 1)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
for epoch in range(100):
    model.train()
    output = model(X_train_tensor)
    loss = criterion(output, y_train_tensor)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
# Evaluate KAN
model.eval()
with torch.no_grad():
    predictions_kan = model(X_test_tensor).numpy()
    predictions_kan = scaler.inverse_transform(predictions_kan)
    y_test_actual = scaler.inverse_transform(y_test)

# Fit ARIMA on original values
train_arima = df["value"].iloc[:train_size + window_size]
test_arima = df["value"].iloc[train_size + window_size:]
model_arima = ARIMA(train_arima, order=(5, 1, 0)).fit()
predictions_arima = model_arima.forecast(steps=len(test_arima))

mse_kan = mean_squared_error(y_test_actual, predictions_kan)
rmse_kan = np.sqrt(mse_kan)
mse_arima = mean_squared_error(test_arima.values, predictions_arima.values)
rmse_arima = np.sqrt(mse_arima)

# Create RMSE comparison table
rmse_df = pd.DataFrame({
    "Model": ["KAN", "ARIMA"],
    "RMSE": [rmse_kan, rmse_arima]
})






# Minimalist style configuration (inspired by Edward Tufte)
def minimalist_plot_setup():
    plt.rcParams.update({
        "font.family": "serif",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.spines.left": True,
        "axes.spines.bottom": True,
        "axes.labelsize": 12,
        "xtick.labelsize": 10,
        "ytick.labelsize": 10,
    })
# Plot 1: Predicted vs Actual (Test Set)
minimalist_plot_setup()
plt.figure(figsize=(8, 5))
plt.plot(y_test_actual, label="Actual", linewidth=1.2)
plt.plot(predictions_kan, label="Predicted (KAN)", linestyle="--", linewidth=1.2)
plt.xlabel("Time Index (Test Set)")
plt.ylabel("Retail Sales")
plt.title("KAN Forecast vs Actual (Test Set)")
plt.legend(frameon=False)
plt.savefig("kan_vs_actual_testset.png", bbox_inches='tight')
plt.show()
# Plot 2: Recursive Forecast (Next 24 Months)
steps_ahead = 24
last_known_scaled = scaled_values[-window_size:].flatten()
forecast_scaled = []
model.eval()
with torch.no_grad():
    for _ in range(steps_ahead):
        input_tensor = torch.tensor(last_known_scaled.reshape(1, -1), dtype=torch.float32)
        pred = model(input_tensor).item()
        forecast_scaled.append(pred)
        last_known_scaled = np.append(last_known_scaled[1:], pred)
forecast_unscaled = scaler.inverse_transform(np.array(forecast_scaled).reshape(-1, 1))
# Prepare future dates
last_date = df["date"].iloc[-1]
future_dates = pd.date_range(start=last_date + pd.DateOffset(months=1), periods=steps_ahead, freq='MS')
# Plot 2
minimalist_plot_setup()
plt.figure(figsize=(8, 5))
plt.plot(df["date"], df["value"], label="Historical", linewidth=1.2)
plt.plot(future_dates, forecast_unscaled, label="Forecast (KAN)", linestyle="--", linewidth=1.2)
plt.xlabel("Date")
plt.ylabel("Retail Sales")
plt.title("KAN Forecast (Next 2 Years)")
plt.legend(frameon=False)
plt.savefig("kan_forecast_future.png", bbox_inches='tight')
plt.show()