本文介绍了FEDformer，这是一种专为时间序列预测设计的新型结构化Transformer模型。通过将季节性趋势分解和傅里叶变换技术融入传统的Transformer框架中，FEDformer能够更有效地捕捉时间序列数据中的全局结构和长期依赖关系。与标准的基于Transformer的架构相比，该模型在实现最先进的预测精度的同时，还显著降低了计算开销。

背景

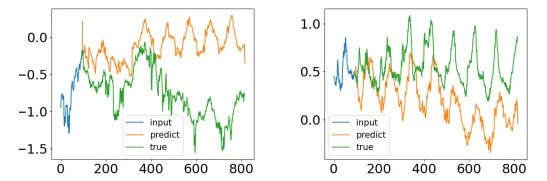
基于Transformer的架构已成为时间序列预测领域最新进展的支柱，这得益于它们在自然语言处理等领域的成功应用。然而，尽管标准Transformer模型具有很强的预测能力，但它们也面临着显著的局限性，包括高计算复杂度和大量的内存需求。更为关键的是，这些模型在保留时间序列数据的全局统计特性方面往往存在困难——这一缺陷在长期预测任务中尤为明显。如上图所示，这些问题会导致预测性能随时间显著下降。

为了应对这些挑战，作者从序列数据分析中成熟的信号处理技术中汲取灵感——具体来说，就是季节性趋势分解、傅里叶域分析和小波变换。这些方法不仅计算效率高，而且能够有效地捕捉时间序列中的关键模式，因此为改进基于Transformer的预测模型奠定了坚实的基础。

方法

频域中的时间序列

作者采用傅里叶分析方法应用于神经网络。需要注意的是，如何使用傅里叶方法恰当地表示时间序列中的信息至关重要。例如，在频域中保留所有元素可能会导致由于噪声实例而导致的表示效果不佳，而仅处理低频分量则会导致预测模型拟合不足。作者专注于选择少量能够紧凑表示整个时间序列的傅里叶分量。

在本文中，m个时间序列表示为X₁(t), …, Xₘ(t)。每个元素通过傅里叶变换方法转换为一个向量aᵢ = (aᵢ,₁, …, aᵢ,ₔ)⊤ ∈ ℝᵈ。最终，本文中的多元时间序列被表示为一个单一矩阵A = (a₁, a₂, … , aₘ)ᐪ ∈ ℝᵐᕽᵈ。

作者从这d个傅里叶分量中均匀随机地选择s个元素。作者通过掩码矩阵S ∈ {0, 1}ˢᕽᵈ来实现选择方式，其中1表示元素被包含，0表示不包含。然后，多元时间序列的表示变为A’ = ASᐪ ∈ ℝᵐᕽˢ。实际上，A’可以表达A的大部分信息。

为了评估A’的保留情况，将A的每个列向量投影到由A的列向量张成的子空间中。这一过程表示为Pₐ(A)，其中Pₐ(·)是投影算子。A和Pₐ(A)之间的误差越小，表示A’保留了A的大部分信息。

对于现实世界中的多元时间序列，它们不仅依赖于其过去的值，而且彼此之间也存在依赖关系，并且共享相似的频率分量。作者强调，随机选择傅里叶分量的一个子集可以恰当地表示傅里叶矩阵A中的信息。这一强调基于以下定理。

定理1。假设矩阵A的一致性度量?(A)为Ω(k/n)。那么，在大概率下，我们有

|A — Pₐ(A)| ≤ (1 + ϵ)|A - Aₖ|

如果s = O(k² / ϵ²)

其中，Aₖ表示A通过其前k个最大奇异值分解得到的近似。

模型

FEDformer框架

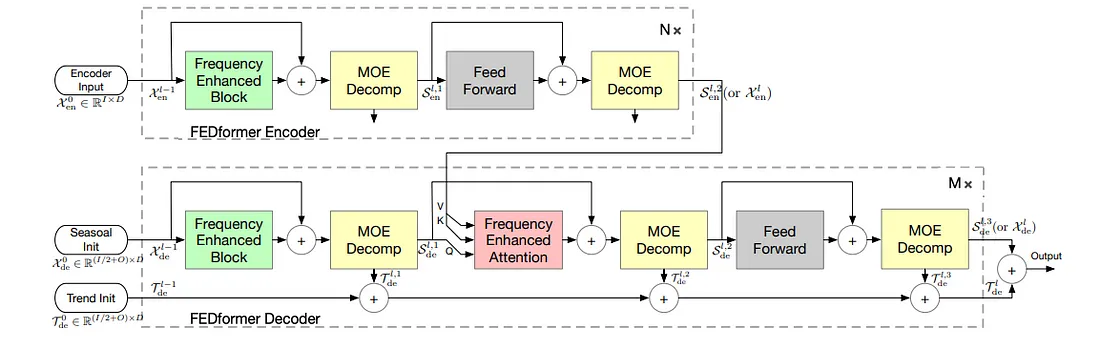
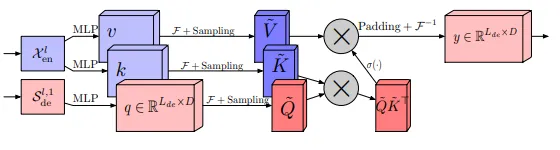
作者基于所提出的傅里叶分析方法，提出了FEDformer（Frequency Enhanced Decomposed Transformer，频率增强分解Transformer）模型。在该模型中，傅里叶分析方法通过频率增强块（Frequency Enhanced Block，FEB）和频率增强注意力（Frequency Enhanced Attention，FEA）得以实现。序列分解方式则通过专家混合分解块（Mixture Of Experts Decomposition block，MOEDecomp）来实现。该模型在给定长度为I的输入和隐藏状态D的情况下，返回长度为O的输出，其中编码器的输入是一个I × D的矩阵，而解码器有(I/2 + O) × D的输入。该模型的整体架构如上图所示。

FEDFormer的编码器公式化表示如下。

注意，Xₑₙˡ = Encoder(Xₑₙˡ⁻¹) 表示第 l 层编码器的输出，而 Xₑₙ⁰ ∈ ℝᴵᕽᴰ 是嵌入后的历史序列。第 l 层中第 i 个分解块之后的季节性成分表示为 Sₑₙˡᣟ¹，其中 i ∈ {1, 2}。特别地，在本工作中，FEB 模块有两个不同版本，即通过离散傅里叶变换（DFT）和离散小波变换（DWT）实现的 FEB-f 和 FEB-w。

FEDFormer 的解码器公式化表示如下。

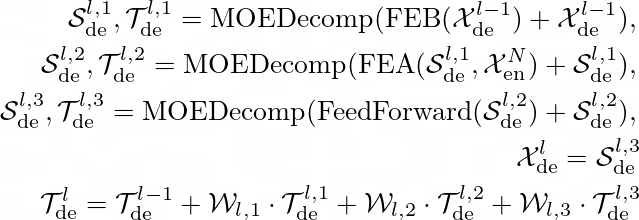
这里，?ₔₑ ˡ ᣟ¹ , ?ₔₑ ˡ ᣟ¹, i ∈ {1, 2, 3} 表示第 l层中第 i个分解块之后的季节和趋势成分。?ₗ,₁ , i ∈ {1, 2, 3}表示针对第 i个提取趋势?ₔₑ ˡ ᣟ¹的投影仪。第 l 层解码器的最终输出为 ?ₔₑ ˡ和?ₔₑ ˡ。

最终预测结果是两个精炼分解成分的和，即 ?ₛ · ?ₜₑᴹ + ?ₜₑᴹ，其中 ?ₛ 表示将深度变换后的季节性成分 ?ₜₑᴹ 投影到目标维度。

傅里叶增强结构

——离散傅里叶变换（DFT）

作者将离散傅里叶变换表示为Xₗ = ∑ₙ₌₀ᴺ⁻¹ x ₙe⁻ ᶦʷˡⁿ，将逆变换表示为x ₙ = ∑ₙ₌₀ᴺ⁻¹ Xₗ e ᶦʷˡⁿ。通过在 DFT 和逆 DFT 之前选择索引，计算复杂度可以进一步降低至 O( N )。

—— 基于傅里叶变换的频率增强块（FEB-f）

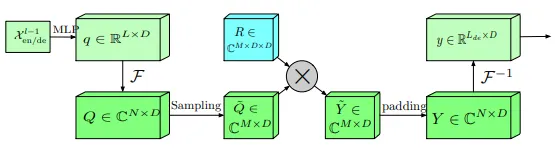
FEB-f 块表示对输入序列进行傅里叶变换。首先，从输入向量 ? 和参数 ? 中收集线性变换后的向量 ?。傅里叶变换的结果表示为 ? ∈ ℂᴺᕽᴰ。在 ? 中的选择过程表示如下。

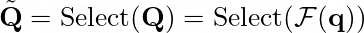
这里，˜? ∈ ℂ ᴹ ᕽᴰ 且M << N。最后，FEB-f 定义为

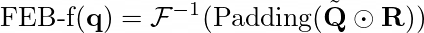
其中，ℝ ∈ ℂᴰᕽᴰᕽᴹ 表示一个随机初始化的参数化核函数。乘积运算符 ⊙ 表示按参数相乘后的求和。该操作的结果随后被零填充到 ℂᴺᕽᴰ（即维度为N×D的复数空间）后，再执行逆傅里叶变换回到时域。

—— 基于傅里叶变换的频率增强注意力（FEA-f）

FEA-f 是结合傅里叶变换对标准注意力机制进行修改后的版本。它在频域中执行其过程。FEA-f 的定义如下。

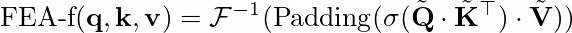
符号?表示激活函数，?、?和?分别表示标准注意力系统中的查询（Query）、键（Key）和值（Value）。FEA-f的结构如上图所示。

小波增强结构

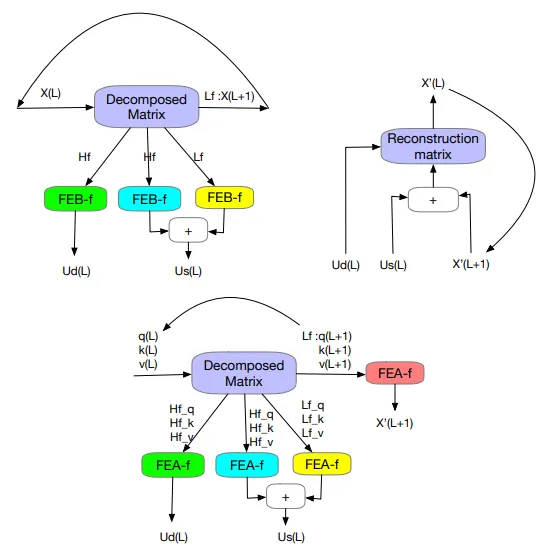
—— 离散小波变换（DWT）

本文中的小波变换生成了信号在频域和时域的表示，这允许高效地访问信号的局部信息。DWT的应用机制如上图所示。

—— 基于小波变换的频率增强块（FEB-w）

FEB-w的输入首先被递归地分解为3个部分，并分别进行处理。具体来说，小波分解部分隐含了固定的勒让德小波基分解矩阵。分离出的3个部分是小波分解得到的高频部分、低频部分和剩余部分。

—— 基于小波变换的频率增强注意力（FEA-w）

在FEA-w中，分解过程分别对?、?、?信号进行。作者采用了一种直接的方法，用小波分解构建频率增强的交叉注意力，将每个FEB-f模块替换为FEA-w模块。

用于季节性-趋势分解的专家混合

作者设计了一个专家混合分解块（MOEDecomp）。该块包含一组不同大小的平均滤波器，用于从输入信号中提取多个趋势成分，以及一组数据依赖的权重，用于将它们组合成最终的趋势。

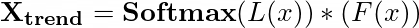
此处，F(·) 表示一组平均池化滤波器，而 Softmax(L(x)) 表示用于混合这些提取出的趋势的权重。

复杂度分析

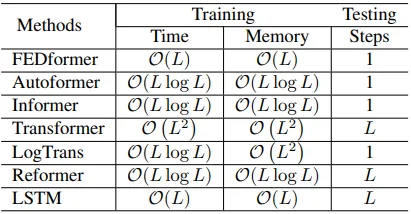
与其他需要更多时间和内存资源的Transformer模型相比，所提出的FEDformer在时间和内存需求方面均实现了O(L)复杂度。

实验

作者进行了广泛的实验，以评估所提出的FEDformer在预测性能方面的表现。

数据集

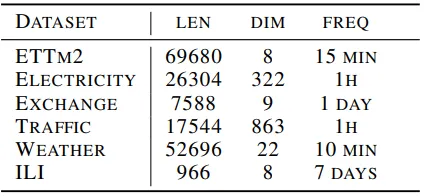
本研究采用了6个用于时间序列预测任务的公开数据集。这6个数据集均包含多元时间序列。在实验中，数据集按照7:1:2的比例被划分为训练集、验证集和测试集。数据集的汇总信息上图所示。

• 输入长度：96
• 预测长度：96、192、336、720

模型设置

• 优化器：Adam
• — 学习率：0.0001
• 批量大小：32

评估指标

本研究采用均方误差（MSE）和平均绝对误差（MAE）进行预测评估。所有实验均重复5次，最终结果采用这些指标的平均值。

结果

多元案例

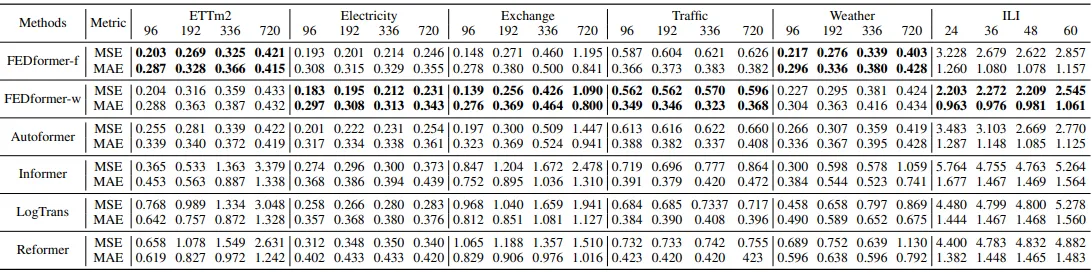
作者将两种FEDformer模型与其他现有方法（如Autoformer）进行了比较。多元预测实验的结果如上图所示。以下误差表示比其他Transformer技术更好的预测性能。需要注意的是，存在不同的FEDformer变体，它们能更准确地表示特定的数据集。

单变量案例

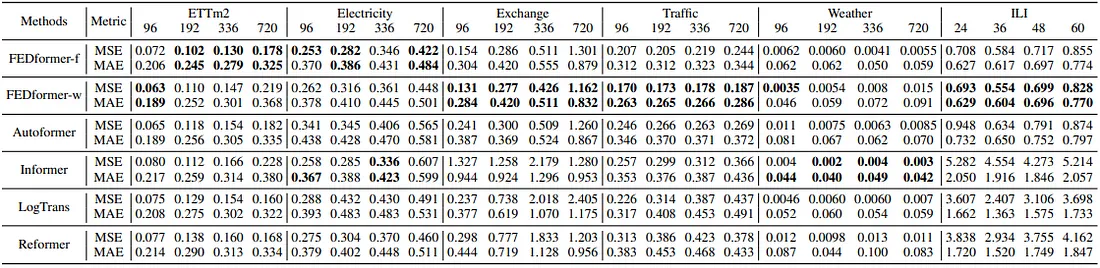
本研究还进行了单变量时间序列预测测试。相应的结果如上图所示。除了Informer的一些结果外，FEDformer模型表现出更好的预测性能。

FEDformer变体的消融研究

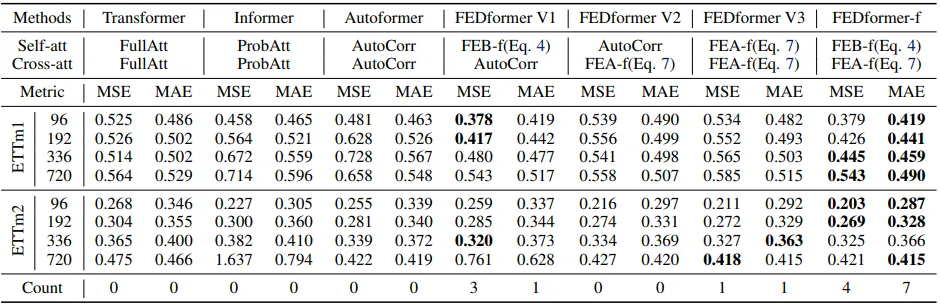
作者设计了一项消融研究，通过修改所提出的FEDformer来实现，修改后的模型如下：

• FEDformer V1：仅使用FEB替换自注意力机制
• FEDformer V2：仅使用FEB替换交叉注意力机制
• FEDformer V3：同时使用FEB替换自注意力机制和交叉注意力机制

实验结果如上图所示。相应的性能表明，FEB中的自注意力机制和交叉注意力机制均能有效提高准确性。

模式选择策略

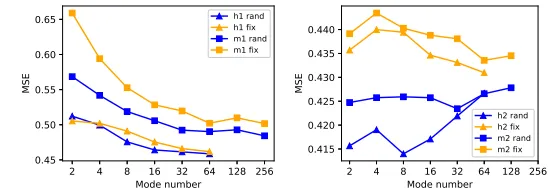
作者通过实证比较了随机选择策略与固定选择策略，以验证随机傅里叶模式选择方式的优越性，并将测试结果总结在图11中。所采用的随机策略比常见的固定策略取得了更好的性能。

预测输出的分布分析

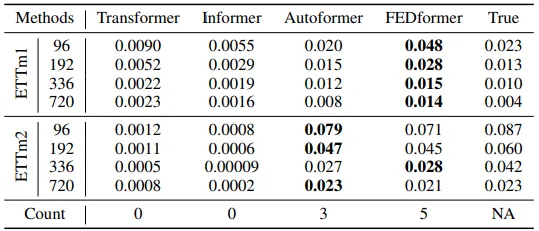
作者定量评估了不同Transformer网络输入与预测之间的分布相似性。根据ETTm数据集进行的Kolmogorov-Smirnov检验结果如上图所示。结果表明，与其他模型相比，FEDformer与输入序列的分布更为相似。

结论

本研究通过提出一种基于Transformer的新型架构，将频域分析集成其中以提高预测性能，在长期时间序列预测方面迈出了重要一步。通过利用傅里叶和小波域中时间序列的稀疏性和低秩特性，FEDformer实现了更紧凑且信息丰富的表示，从而提高了准确性并降低了计算成本。在多个基准数据集上，FEDformer始终优于现有的最先进模型，证明了其在捕捉时间序列数据中的长距离依赖关系和全局模式方面的有效性。