你需要了解的关于神经网络的所有知识
2017年11月04日 由 yuxiangyu 发表
332187
0
进行机器学习的很多人容易被神经网络中的各种名词或者概念搞懵,这篇文章将带你了解这些名词或者概念的含义,以便你能更好更全面的了解它们。
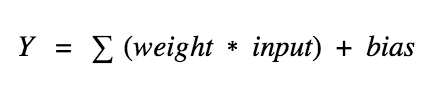 神经元(Node):
神经元(Node):它是神经网络的基本单位。它获得一定数量的输入和一个偏置值。当信号(值)到达时会乘以一个权值。如果神经元有4个输入,那么就有4个权值,权重可以在训练时调整。
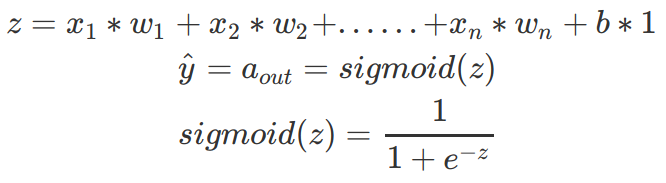
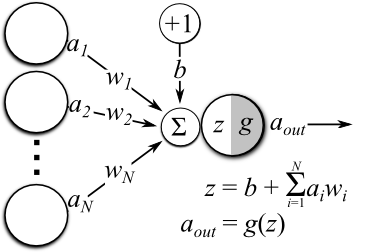
神经网络中单个神经元的运作
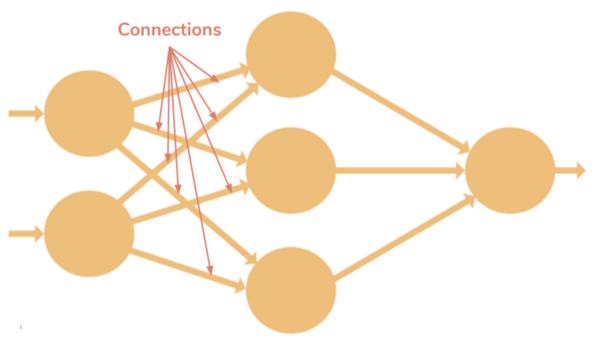
连接:它将一个神经元连接到另一层或同一层的另一个神经元。连接伴随着与之相关联的权值。训练的目标是更新此权值以减少损失(即错误)。
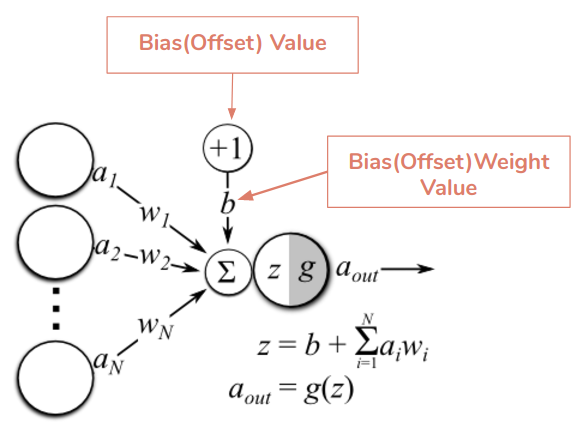 偏置(偏移):
偏置(偏移):它是神经元的额外输入,它始终为1,并具有自己的连接权重。这确保即使所有的输入都为空(全部为0),神经元也会激活。
激活功能(传递函数):激活函数用于将非线性引入神经网络。它会将值缩小到较小的范围内。Sigmoid激活函数的压缩范围为0到1之间。在深度学习中有许多激活函数可用,ReLU,SeLU和TanH均优于Sigmoid激活函数。
在本文中,我已经解释了不同的激活函数。
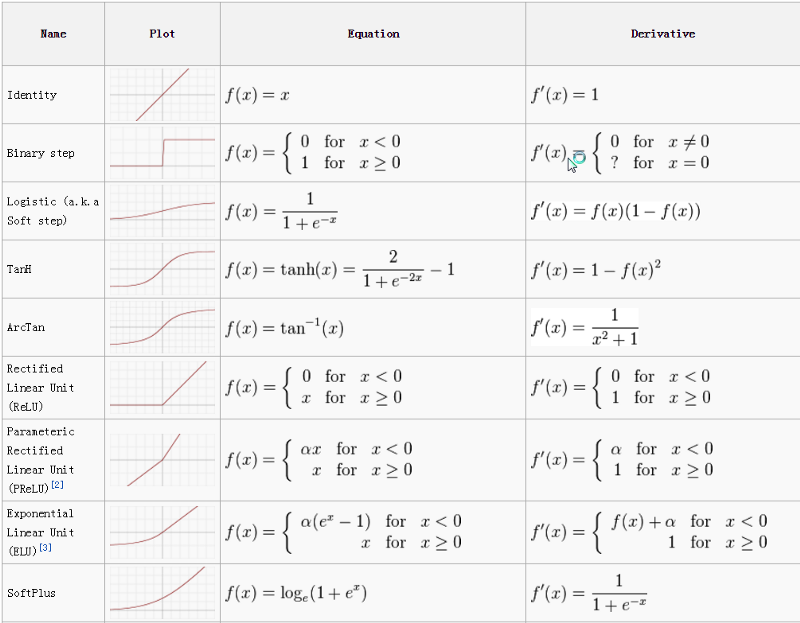
激活函数来源 - http://prog3.com/sbdm/blog/cyh_24/article/details/50593400
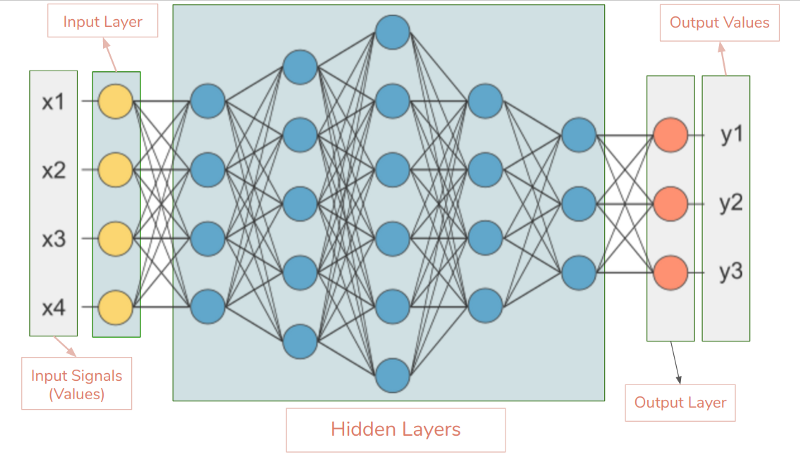
基础的神经网络布局
输入层 :神经网络中的第一层。它需要输入信号(值)并将它们传递到下一层。它不对输入信号(值)做任何操作,并且没有关联的权重和偏置值。在我们的网络中,我们有4个输入信号x1,x2,x3,x4。
隐藏层:隐藏层具有对输入数据应用不同变换的神经元(节点)。一个隐藏层是垂直排列的神经元的集合(Representation)。在我们给出的图像中有5个隐藏层。在我们的网络中,第一隐层有4个神经元(节点),第2层有5个神经元,第3层有6个神经元,第4层有4个,第5层有3个神经元。最后一个隐藏层将值传递给输出层。隐藏层中的每个神经元都与下一层的每一个神经元有连接,因此我们有一个完全连接的隐藏层。
输出层 :着是网络的最后一层,它接收来自最后一个隐藏层的输入。通过这个层,我们可以知道期望的值和期望的范围。在这个网络中,输出层有3个神经元,输出y1,y2,y3。
Input Shape :它是我们传递给输入层的输入矩阵形状。我们网络的输入层有4个神经元,它期望1个样本的4个值。如果我们一次只提供一个样本,我们网络的期望输入形状是(1,4,1)。如果我们提供100个样品,则输入形状将为(100,4,1)。不同的库期望形状的格式是不同的。
权重(参数):权重表示单元之间连接的强度。如果从节点1到节点2的权重比较大,意味着神经元1对神经元2的影响比较大。权重降低了输入值的重要性。当权重接近零时意味着更改此输入将不会更改输出。负权重意味着增加此输入会降低输出。权重决定了输入对输出的影响程度。
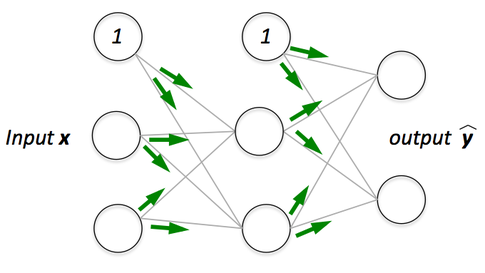
前向传播
前向传播:前向传播的过程是向神经网络馈送输入值并得到我们称为预测值的输出。当我们将输入值提供给神经网络的第一层时,它没有进行任何操作。第二层从第一层获取值并进行乘法,加法和激活操作,然后将得到的值传递给下一层。在后面的层中执行相同的操作,最后我们在最后一层得到一个输出值。
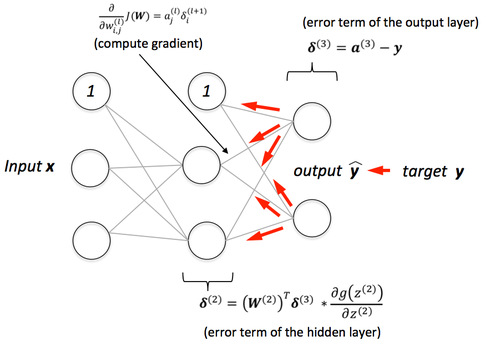
反向传播
反向传播:前向传播后,我们得到一个被称为预测值的输出值。为了计算误差,我们将预测值与实际输出值进行比较。我们使用损失函数(下面会提到)来计算误差值。然后我们计算神经网络中每一个误差值的导数和每一个权重。反向传播使用微分学的链式法则。在链条法则中,首先我们计算对应最后一层权值的误差值的导数。我们称这些导数为:梯度,然后使用这些梯度值来计算倒数第二层的梯度。重复此过程,直到我们得到神经网络中每个权重的梯度。然后从权值中减去该梯度值,以减少误差值。这样,我们就更接近(下降)局部最小值(也就是说最小的损失)。
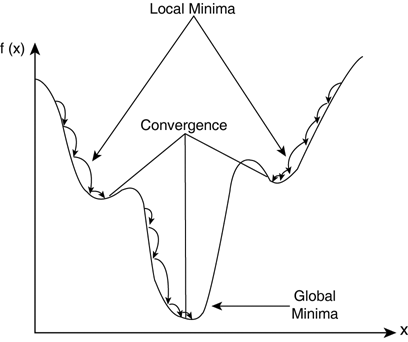
学习率:当我们训练神经网络时,我们通常使用梯度下降法来优化权重。在每次迭代中,我们都使用反向传播来计算每个权重的损失函数的导数,并从这个权重中减去它。学习率决定了你想要更新权重(参数)值的速度。学习率不能太低导致收敛的速度缓慢,也不能太高导致找不到局部最小值。
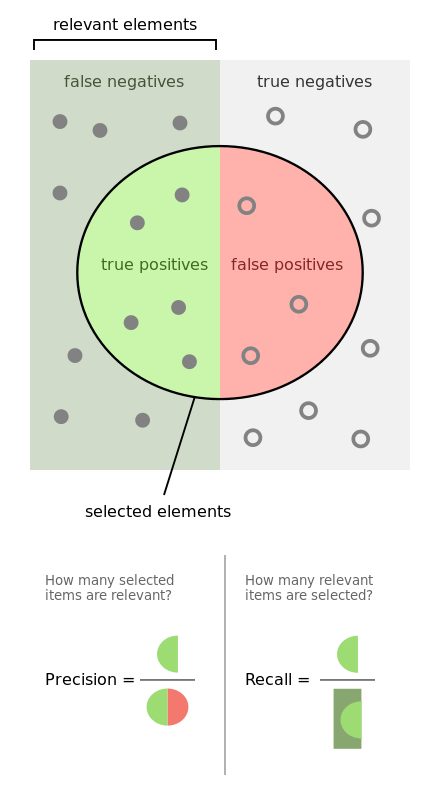 精确率和召回率
精确率和召回率
准确率:准确率是指测量值与标准值或已知值的接近程度。
精确率:精确率是指两个或更多测量值的接近程度。它代表测量的重复性或再现性。
召回率:召回率是指在相关实例总数中已经检索到的相关实例的占比。

Tp是真正的阳性,Tn是真阴性,Fp是假阳性,Fn是假阴性
混淆矩阵 - 维基百科:
在机器学习领域特别是关于统计分类的问题,一个混淆矩阵(也称为误差矩阵),是一种特定的表格布局,它让你可以将算法的性能可视化(通常在监督学习中使用,在无监督学习它通常称为匹配矩阵)。矩阵的每一行表示预测类中的实例,而每一列表示实际类中的实例(反之亦然)。这个名字源于这样一个事实:它很容易看出系统是否混淆了两个类(通常是错误地标记成另一个)。
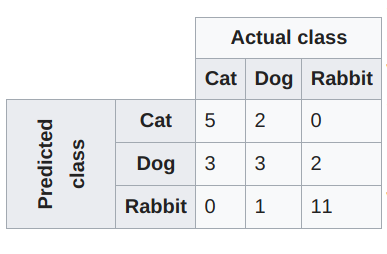
混淆矩阵
收敛:收敛是指迭代进行时输出越来越接近特定值。
正则化 :用于克服过拟合问题。在正则化中,我们通过在权重向量w(它是给定算法中的学习参数的向量)中添加L1(LASSO)或L2(Ridge)范数来惩罚我们的损失项。
L(损失函数)+ λN(w) - 这里λ是你的正则项,N(w)是L1或L2范数
归一化:数据归一化是将一个或多个属性重新调整到0到1的范围的过程。当你不知道数据的分布或者当你知道分布不是高斯函数(钟形曲线)时,归一化是一种很好的解决方法。它有助于加速学习过程。
全连接层 : 当一层中的所有节点的激活进入下一层中的每个节点时。当第L层中的所有节点连接到第(L + 1)层中的所有节点时,我们将这些层称为完全连接的层。
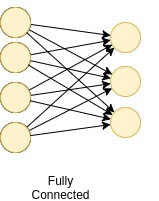
全连接层
损失函数/代价函数: 损失函数计算单个训练示例的误差。代价函数是整个训练集的损失函数的平均值。
- mse:均方误差。
- binary_crossentropy:用于二进制对数损失(logloss)。
- categorical_crossentropy:用于多类的对数损失(logloss)。
模型优化器:优化器是一种用于更新模型中权重的搜索技术。
- SGD:随机梯度下降,支持动量。
- RMSprop:由Geoff Hinton提出的自适应学习率优化方法。
- Adam: Adaptive Moment Estimation (Adam自适应时刻估计方法),能计算每个参数的自适应学习率。
性能指标:性能指标用于测量神经网络的性能。准确率,损失,验证精度,验证损失,平均绝对误差,精确率,召回率和f1分数都是一些性能指标。
批量尺寸 :通过前向或反向训练的示例数。批量尺寸越大,你需要的内存空间就越大。
训练次数:模型接触训练数据集的次数。每一次等于一次通过前向或反向的所有训练实例。





















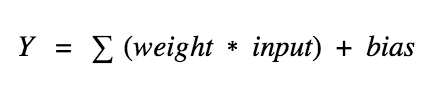
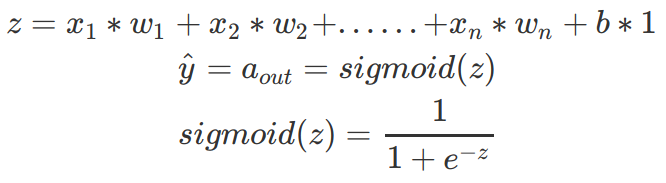








 精确率和召回率
精确率和召回率












