开始使用新数据集时，最好先进行一些探索性数据分析（EDA）。在训练任何花哨的模型之前，花点时间了解你的数据，可以帮助你了解数据集的结构，识别任何明显的问题，并应用特定领域的知识。

在本文中，我们将使用协方差矩阵、聚类、PCA 和向量数学等技术，将 EDA 应用于 GloVe 词嵌入。这将帮助我们理解词嵌入的结构，为我们利用这些数据建立更强大的模型提供一个有用的起点。在发现这种结构的过程中，我们会发现它并不总是像看上去那样，而且语料库中还隐藏着一些令人惊讶的偏差。

数据集

要开始学习，请从 huggingface.co/stanfordnlp/glove/resolve/main/glove.6B.zip[1] 下载数据集。其中包含三个文本文件，每个文件都包含单词列表及其向量表示。我们将使用 300 维表示法（glove.6B.300d.txt）。

简要说明一下这个数据集的来源：从本质上讲，这是一个单词嵌入列表，由维基百科和各种新闻来源中价值 60 亿的共现数据生成。使用共现的一个有用的副作用是，意思相近的词往往会靠近在一起。例如，由于 “红色的鸟 ”和 “蓝色的鸟 ”都是有效的句子，因此我们可以预期 “红色 ”和 “蓝色 ”的向量会相互接近。

需要明确的是，这些并不是为大型语言模型而训练的词嵌入。它们是基于大型语料库的完全无监督技术。但它们显示出与语言模型嵌入很多相似的特性，而且本身也很有趣。

该文本文件的每一行由一个单词组成，后面是相关嵌入的全部 300 个向量分量，并用空格隔开。我们可以用 Python 加载它。(为了减少噪音和加快速度，我在这里使用了全部数据集的前 10%（/10），但你可以根据需要进行更改）。

import numpy as np
embeddings = {}
with open(f"glove.6B/glove.6B.300d.txt", "r") as f:
    glove_content = f.read().split('\n')
for i in range(len(glove_content)//10):
    line = glove_content[i].strip().split(' ')
    if line[0] == '':
        continue
    word = line[0]
    embedding = np.array(list(map(float, line[1:])))
    embeddings[word] = embedding
print(len(embeddings))

这样，我们就加载了 40,000 个嵌入。

相似性度量

我们可能会问的一个自然问题是：向量是否通常与其他具有相似意义的向量接近？作为一个后续问题，我们如何量化这个问题呢？

我们量化向量间相似性的方法主要有两种：一种是欧氏距离，也就是我们熟悉的勾股定理距离。另一种是余弦相似度，它测量的是两个向量之间夹角的余弦值。一个向量与自身的余弦相似度为 1，与相反向量的余弦相似度为-1，与正交向量的余弦相似度为 0。

让我们在 NumPy 中实现这些功能：

def cos_sim(a, b):
    return np.dot(a,b)/(np.linalg.norm(a) * np.linalg.norm(b))
def euc_dist(a, b):
    return np.sum(np.square(a - b)) # no need for square root since we are just ranking distances

现在，我们可以找到与给定单词或嵌入向量最接近的所有向量！我们将按递增顺序进行。

def get_sims(to_word=None, to_e=None, metric=cos_sim):
    # list all similarities to the word to_word, OR the embedding vector to_e
    assert (to_word is not None) ^ (to_e is not None) # find similarity to a word or a vector, not both
    sims = []
    if to_e is None:
        to_e = embeddings[to_word] # get the embedding for the word we are looking at
    for word in embeddings:
        if word == to_word:
            continue
        word_e = embeddings[word]
        sim = metric(word_e, to_e)
        sims.append((sim, word))
    sims.sort()
    return sims

现在我们可以编写一个函数来显示 10 个最相似的单词。如果能加入一个反向选项，我们就可以显示最不相似的单词了。

def display_sims(to_word=None, to_e=None, n=10, metric=cos_sim, reverse=False, label=None):
    assert (to_word is not None) ^ (to_e is not None)
    sims = get_sims(to_word=to_word, to_e=to_e, metric=metric)
    display = lambda sim: f'{sim[1]}: {sim[0]:.5f}'
    if label is None:
        label = to_word.upper() if to_word is not None else ''
    print(label) # a heading so we know what these similarities are for
    if reverse:
        sims.reverse()
    for i, sim in enumerate(reversed(sims[-n:])):
        print(i+1, display(sim))
    return sims

最后，我们可以对其进行测试！

display_sims(to_word='red')'red')
# yellow, blue, pink, green, white, purple, black, colored, sox, bright

看来波士顿红袜队出人意料地出现在了这里。除此以外，这和我们预想的差不多。

也许我们可以尝试一些动词，而不仅仅是名词和形容词？像 “分享 ”这样好听又亲切的动词怎么样？

display_sims(to_word='share')'share')
# shares, stock, profit, percent, shared, earnings, profits, price, gain, cents

我想，在这个数据集中，“分享 ”并不常用作动词。哦，好吧。

我们还可以尝试一些更常规的例子：

display_sims(to_word='cat')'cat')
# dog, cats, pet, dogs, feline, monkey, horse, pets, rabbit, leopard
display_sims(to_word='frog')
# toad, frogs, snake, monkey, squirrel, species, rodent, parrot, spider, rat
display_sims(to_word='queen')
# elizabeth, princess, king, monarch, royal, majesty, victoria, throne, lady, crown

类比推理

单词嵌入的一个迷人特性是使用向量数学建立类比。GloVe 论文中的例子是国王 - 王后 = 男人 - 女人。换句话说，重新排列等式后，我们认为国王 = 男人 - 女人 + 皇后。这是真的吗？

display_sims(to_e=embeddings['man'] - embeddings['woman'] + embeddings['queen'], label='king-queen analogy')'man'] - embeddings['woman'] + embeddings['queen'], label='king-queen analogy')
# queen, king, ii, majesty, monarch, prince...

不完全是：与男人-女人+皇后最接近的向量是皇后（余弦相似度 0.78），其次是国王（余弦相似度 0.66）。受 3Blue1Brown 这段精彩视频的启发，我们不妨试试姨妈和姨夫：

display_sims(to_e=embeddings['aunt'] - embeddings['woman'] + embeddings['man'], label='aunt-uncle analogy')'aunt'] - embeddings['woman'] + embeddings['man'], label='aunt-uncle analogy')
# aunt, uncle, brother, grandfather, grandmother, cousin, uncles, grandpa, dad, father

这个结果要好一些（余弦相似度 0.7348 对 0.7344），但效果仍不理想。不过，我们可以尝试改用欧氏距离。现在我们需要设置 reverse=True，因为欧氏距离越大，相似度越低。

display_sims(to_e=embeddings['aunt'] - embeddings['woman'] + embeddings['man'], metric=euc_dist, reverse=True, label='aunt-uncle analogy')'aunt'] - embeddings['woman'] + embeddings['man'], metric=euc_dist, reverse=True, label='aunt-uncle analogy')
# uncle, aunt, grandfather, brother, cousin, grandmother, newphew, dad, grandpa, cousins

现在我们明白了。不过，看起来数学类比可能并不像我们希望的那样完美，至少我们在这里用的是天真的方法。

角度

余弦相似度的核心是向量之间的夹角。但向量的大小是否也很重要呢？

我们可以重新使用现有的代码，将幅值表示为与零向量的欧氏距离。让我们看看哪些词的幅值最大和最小：

zero_vec = np.zeros_like(embeddings['the'])'the'])
display_sims(to_e=zero_vec, metric=euc_dist, label='largest magnitude')
# republish, nonsubscribers, hushen, tael, www.star, stoxx, 202-383-7824, resend, non-families, 225-issue
display_sims(to_e=zero_vec, metric=euc_dist, reverse=True, label='smallest magnitude')
# likewise, lastly, interestingly, ironically, incidentally, moreover, conversely, furthermore, aforementioned, wherein

大量级矢量的含义似乎没有什么规律可循，但它们似乎都有非常具体（有时甚至令人困惑）的含义。另一方面，最小量级向量往往是非常常见的词，可以在各种语境中找到。

幅值之间的范围很大：从最小矢量的 2.6 到最大矢量的 17。这种分布是什么样的呢？我们可以绘制直方图来更好地了解这一情况。

import matplotlib.pyplot as plt
def plot_magnitudes():
    words = [w for w in embeddings]
    magnitude = lambda word: np.linalg.norm(embeddings[word])
    magnitudes = list(map(magnitude, words))
    plt.hist(magnitudes, bins=40)
    plt.show()
plot_magnitudes()

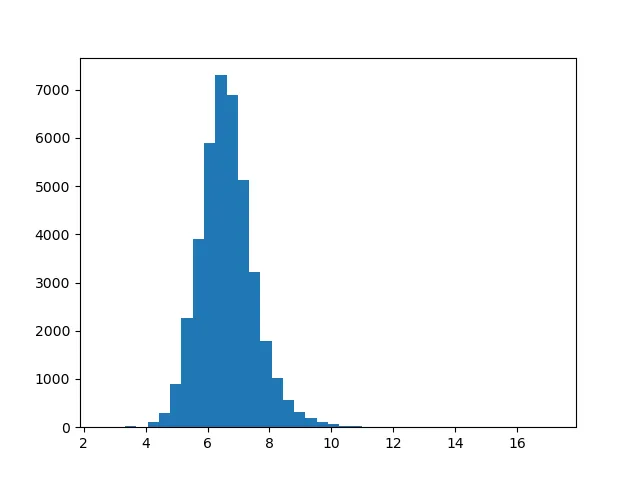
这种分布看起来近似正态分布。如果我们想进一步检验，可以使用 Q-Q 图。但对于我们现在的目的来说，这样就可以了。

数据集偏差

事实证明，向量嵌入中的方向和子空间可以对各种概念进行编码，而且通常是有偏差的。

我们也可以在 GloVe 嵌入中复制这一概念。首先，让我们找到 “男性气质 ”概念的方向。我们可以通过取他和她，男人和女人等向量之间差异的平均值来实现这一目标：

gender_pairs = [('man', 'woman'), ('men', 'women'), ('brother', 'sister'), ('he', 'she'),'man', 'woman'), ('men', 'women'), ('brother', 'sister'), ('he', 'she'),
                    ('uncle', 'aunt'), ('grandfather', 'grandmother'), ('boy', 'girl'),
                    ('son', 'daughter')]
masc_v = zero_vec
for pair in gender_pairs:
    masc_v += embeddings[pair[0]]
    masc_v -= embeddings[pair[1]]

现在，我们可以根据嵌入空间的判断，找到 “最男性化 ”和 “最女性化 ”的向量。

display_sims(to_e=masc_v, metric=cos_sim, label='masculine vecs')'masculine vecs')
# brother, colonel, himself, uncle, gen., nephew, brig., brothers, son, sir
display_sims(to_e=masc_v, metric=cos_sim, reverse=True, label='feminine vecs')
# actress, herself, businesswoman, chairwoman, pregnant, she, her, sister, actresses, woman

现在，我们可以进行一个简单的测试来检测数据集中的偏差：计算护士与男人和女人之间的相似度。从理论上讲，这两个词的相似度应该差不多：护士不是一个有性别区分的词。事实果真如此吗？

print("nurse - man", cos_sim(embeddings['nurse'], embeddings['man'])) # 0.24
print("nurse - woman", cos_sim(embeddings['nurse'], embeddings['woman'])) # 0.45

聚类

让我们看看能否使用 k-means 聚类对意义相似的单词进行聚类。使用 scikit-learn 软件包很容易做到这一点。我们将使用 300 个聚类，这听起来很多，但相信我：几乎所有的聚类都非常有趣，你可以写一整篇文章来解读它们！

from sklearn.cluster import KMeans
def get_kmeans(n=300):
    kmeans = KMeans(n_clusters=n, n_init=1)
    X = np.array([embeddings[w] for w in embeddings])
    kmeans.fit(X)
    return kmeans
def display_kmeans(kmeans):
    # print all clusters and 5 associated words for each
    words = np.array([w for w in embeddings])
    X = np.array([embeddings[w] for w in embeddings])
    y = kmeans.predict(X) # get the cluster for each word
    for cluster in range(kmeans.cluster_centers_.shape[0]):
        print(f'KMeans {cluster}')
        cluster_words = words[y == cluster] # get all words in each cluster
        for i, w in enumerate(cluster_words[:5]):
            print(i+1, w)
kmeans = get_kmeans()
display_kmeans(kmeans)

这里有很多东西值得一看。例如纽约市 ( manhattan, n.y., brooklyn, hudson, borough)、分子生物学 ( protein, proteins, enzyme, beta, molecules) 和印度人名 ( singh, ram, gandhi, kumar, rao)。

但有时这些聚类并不像它们看起来那样。让我们编写代码，显示包含给定单词的聚类中的所有单词，以及最近和最远的聚类。

def get_kmeans_cluster(kmeans, word=None, cluster=None):
    # given a word, find the cluster of that word. (or start with a cluster index.)
    # then, get all words of that cluster.
    assert (word is None) ^ (cluster is None)
    if cluster is None:
        cluster = kmeans.predict([embeddings[word]])[0]
    words = np.array([w for w in embeddings])
    X = np.array([embeddings[w] for w in embeddings])
    y = kmeans.predict(X)
    cluster_words = words[y == cluster]
    return cluster, cluster_words
def display_cluster(kmeans, word):
    cluster, cluster_words = get_kmeans_cluster(kmeans, word=word)
    # print all words in the cluster
    print(f"Full KMeans ({word}, cluster {cluster})")
    for i, w in enumerate(cluster_words):
        print(i+1, w)
    # rank all clusters (excluding this one) by Euclidean distance of their centers from this cluster's center
    distances = np.concatenate([kmeans.cluster_centers_[:cluster], kmeans.cluster_centers_[cluster+1:]], axis=0)
    distances = np.sum(np.square(distances - kmeans.cluster_centers_[cluster]), axis=1)
    nearest = np.argmin(distances, axis=0)
    _, nearest_words = get_kmeans_cluster(kmeans, cluster=nearest)
    print(f"Nearest cluster: {nearest}")
    for i, w in enumerate(nearest_words[:5]):
        print(i+1, w)
    farthest = np.argmax(distances, axis=0)
    print(f"Farthest cluster: {farthest}")
    _, farthest_words = get_kmeans_cluster(kmeans, cluster=farthest)
    for i, w in enumerate(farthest_words[:5]):
        print(i+1, w)

现在让我们试试这段代码。

display_cluster(kmeans, 'animal')'animal')
# species, fish, wild, dog, bear, males, birds...
display_cluster(kmeans, 'dog')
# same as 'animal'
display_cluster(kmeans, 'birds')
# same again
display_cluster(kmeans, 'bird')
# spread, bird, flu, virus, tested, humans, outbreak, infected, sars....?

你可能不会每次都得到完全相同的结果：聚类算法是非确定性的。但在很多时候，“鸟类 ”与疾病词而不是动物词相关联。看来原始数据集倾向于在疾病载体的语境中使用 “鸟 ”这个词。

主成分分析

主成分分析（PCA）是一种工具，我们可以用它在向量空间中找到与数据集中最大变异相关的方向。让我们试试吧。就像聚类一样，sklearn 也能轻松完成这项工作。

from sklearn.decomposition import PCA
def get_pca_vecs(n=10): # get the first 10 principal components
    pca = PCA()
    X = np.array([embeddings[w] for w in embeddings])
    pca.fit(X)
    principal_components = list(pca.components_[:n, :])
    return pca, principal_components
pca, pca_vecs = get_pca_vecs()
for i, vec in enumerate(pca_vecs):
    # display the words with the highest and lowest values for each principal component
    display_sims(to_e=vec, metric=cos_sim, label=f'PCA {i+1}')
    display_sims(to_e=vec, metric=cos_sim, label=f'PCA {i+1} negative', reverse=True)

就像我们的 k-means 实验一样，这些 PCA 向量中有很多都非常有趣。例如，我们来看看主成分 9：

    PCA 9
1 featuring: 0.38193
2 hindi: 0.37217
3 arabic: 0.36029
4 sung: 0.35130
5 che: 0.34819
6 malaysian: 0.34474
7 ka: 0.33820
8 video: 0.33549
9 bollywood: 0.33347
10 counterpart: 0.33343
    PCA 9 negative
1 suffolk: -0.31999
2 cumberland: -0.31697
3 northumberland: -0.31449
4 hampshire: -0.30857
5 missouri: -0.30771
6 calhoun: -0.30749
7 erie: -0.30345
8 massachusetts: -0.30133
9 counties: -0.29710
10 wyoming: -0.29613

看起来，成分 9 的正值与中东、南亚和东南亚术语有关，而负值则与北美和英国术语有关。

另一个有趣的是成分 3。所有正项都是十进制数，这显然是该模型的一个显著特征。成分 8 也显示了类似的模式。

    PCA 3
1 1.8: 0.57993
2 1.6: 0.57851
3 1.2: 0.57841
4 1.4: 0.57294
5 2.3: 0.57019
6 2.6: 0.56993
7 2.8: 0.56966
8 3.7: 0.56660
9 1.9: 0.56424
10 2.2: 0.56063

降维

PCA 的主要优点之一是，它允许我们将一个非常高维的数据集（本例中为 300 维），通过投影到第一分量上，绘制成仅有两维或三维的图形。让我们尝试绘制二维图，看看是否能从中收集到任何信息。我们还将使用 k-means 按聚类进行颜色编码。

def plot_pca(pca_vecs, kmeans):
    words = [w for w in embeddings]
    x_vec = pca_vecs[0]
    y_vec = pca_vecs[1]
    X = np.array([np.dot(x_vec, embeddings[w]) for w in words])
    Y = np.array([np.dot(y_vec, embeddings[w]) for w in words])
    colors =  kmeans.predict([embeddings[w] for w in words])
    plt.scatter(X, Y, c=colors, cmap='spring') # color by cluster
    for i in np.random.choice(len(words), size=100, replace=False):
        # annotate 100 randomly selected words on the graph
        plt.annotate(words[i], (X[i], Y[i]), weight='bold')
    plt.show()
plot_pca(pca_vecs, kmeans)

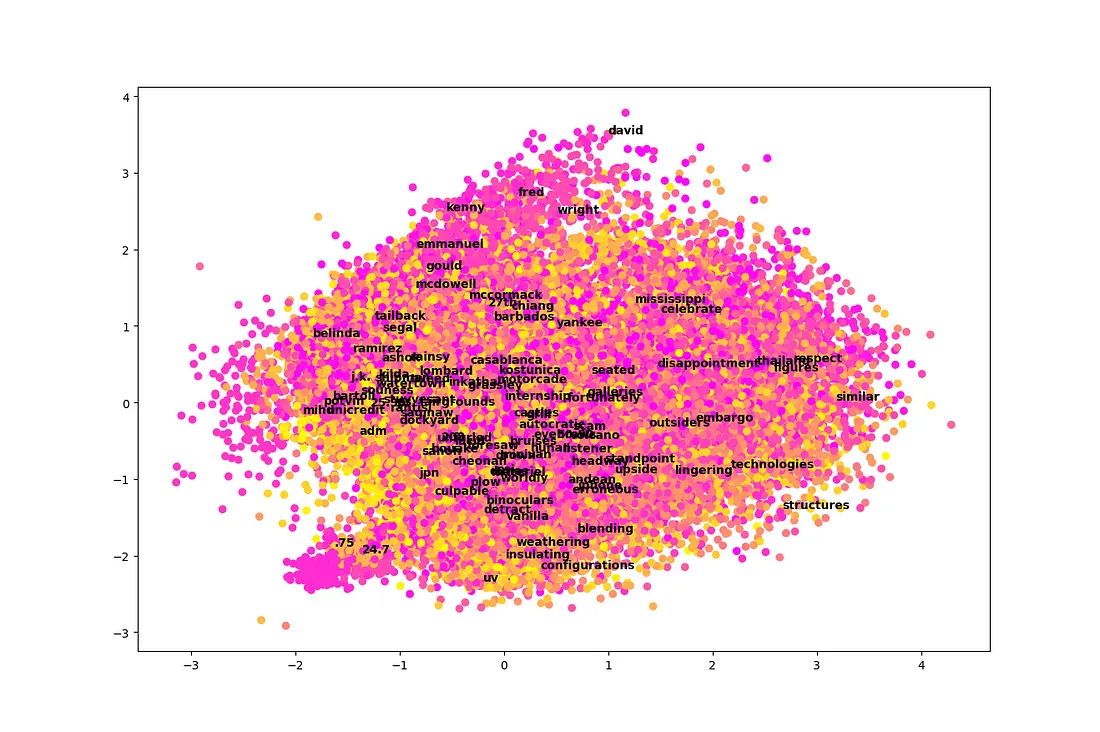
遗憾的是，这个情节完全是一团糟！很难从中学到什么。看起来，在总共 300 个维度中，孤立的两个维度并不容易解读，至少在这个数据集中是这样。

有两个例外。首先，我们可以看到名字往往聚集在图表的顶部附近。其次，左下方有一小块区域非常突出。这个区域似乎与数字有关，尤其是十进制数字。

协方差

了解输入特征之间的协方差通常很有帮助。在这种情况下，我们的输入特征只是难以解释的抽象向量方向。不过，协方差矩阵可以告诉我们有多少信息被实际使用。如果我们看到的协方差很高，这就意味着某些维度之间存在很强的相关性，也许我们可以将维度降低一些。

def display_covariance():
    X = np.array([embeddings[w] for w in embeddings]).T # rows are variables (components), columns are observations (words)
    cov = np.cov(X)
    cov_range = np.maximum(np.max(cov), np.abs(np.min(cov))) # make sure the colorbar is balanced, with 0 in the middle
    plt.imshow(cov, cmap='bwr', interpolation='nearest', vmin=-cov_range, vmax=cov_range)
    plt.colorbar()
    plt.show()
display_covariance()

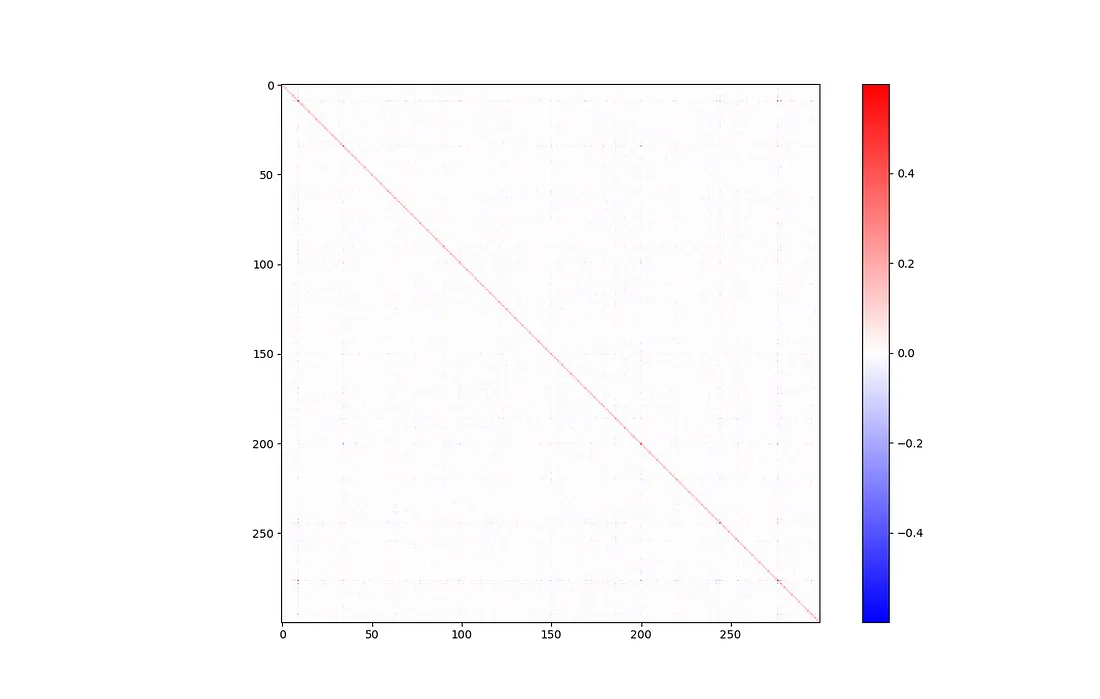
当然，在主要对角线上有一条大线，代表每个成分都与自身密切相关。除此之外，这并不是一张非常有趣的图表。一切看起来都是空白，这是个好兆头。

如果你仔细观察，会发现一个例外：成分 9 和 276 似乎有些强相关（协方差为 0.308）。

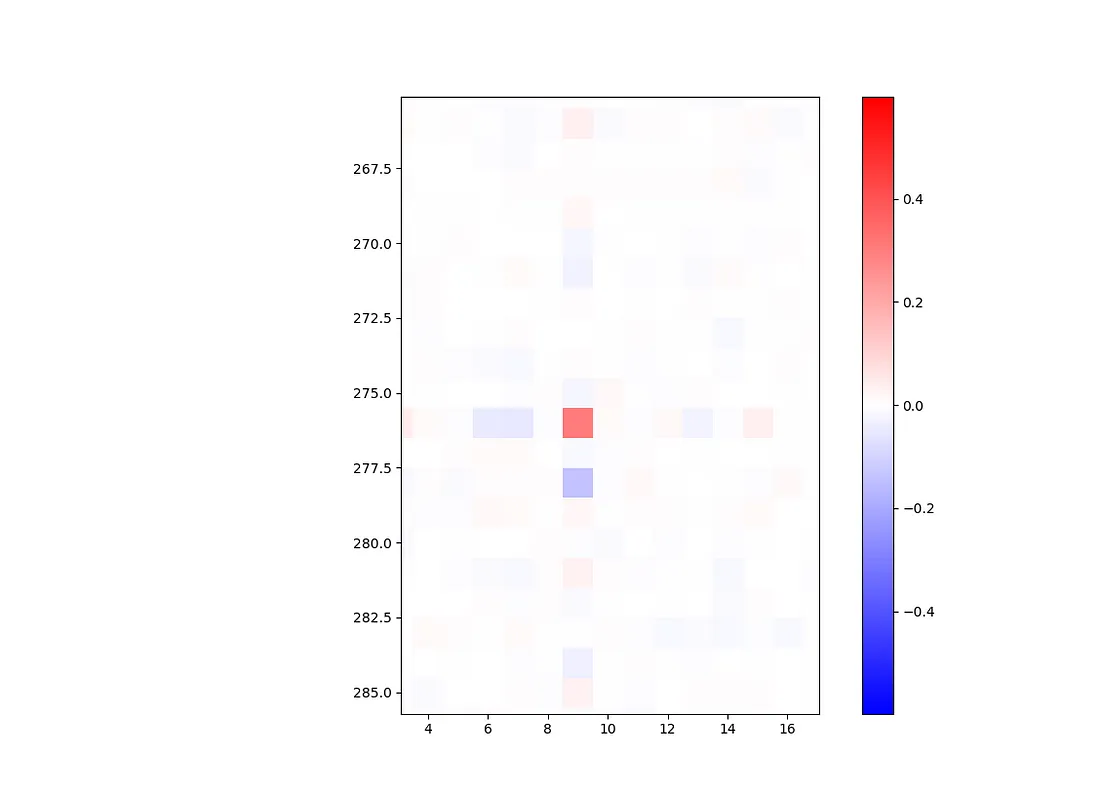
让我们进一步研究这个问题，打印出与 9 和 276 分量最相关的向量。这相当于与一个除相关分量中的 1 外全为 0 的基向量进行余弦相似。

e9 = np.zeros_like(zero_vec)
e9[9] = 1.09] = 1.0
e276 = np.zeros_like(zero_vec)
e276[276] = 1.0
display_sims(to_e=e9, metric=cos_sim, label='e9')
# grizzlies, supersonics, notables, posey, bobcats, wannabe, hoosiers...
display_sims(to_e=e276, metric=cos_sim, label='e276')
# pehr, zetsche, steadied, 202-887-8307, bernice, goldie, edelman, kr...

这些结果很奇怪，信息量也不大。

但是等等：如果在一个成分中数值非常负的词在另一个成分中也往往非常负，那么我们也可以在这些成分中得到正的协方差。让我们试着颠倒一下相似性的方向。

display_sims(to_e=e9, metric=cos_sim, label='e9', reverse=True)'e9', reverse=True)
# therefore, that, it, which, government, because, moreover, fact, thus, very
display_sims(to_e=e276, metric=cos_sim, label='e276', reverse=True)
# they, instead, those, hundreds, addition, dozens, others, dozen, only, outside

看起来，这两个成分都与基本的功能词和数字有关，可以在许多不同的语境中找到。这有助于解释它们之间的协方差，至少比正向情况更能说明问题。

结论

在本文中，我们将各种探索性数据分析（EDA）技术应用于 GloVe 词嵌入的 300 维数据集。我们使用余弦相似度来测量词义之间的相似性，使用聚类将词分成相关的组，并使用主成分分析（PCA）来确定向量空间中对嵌入模型最重要的方向。

通过主成分分析，我们直观地观察到输入特征之间的总体协方差最小。我们尝试使用 PCA 将所有 300 维数据绘制成仅有两个维度的图，但还是有点乱。

我们还测试了数据集中的假设和偏差。通过比较护士与男性和女性的余弦相似度，我们发现了数据集中的性别偏差。我们尝试使用向量数学来表示类比（如 “国王 ”与 “王后 ”的类比，“男人 ”与 “女人 ”的类比），并取得了一些成功。通过减去指代男性和女性的各种向量示例，我们发现了与性别相关的向量方向，并在数据集中显示了 “最男性化 ”和 “最女性化 ”的向量。